相关习题
0 127053 127061 127067 127071 127077 127079 127083 127089 127091 127097 127103 127107 127109 127113 127119 127121 127127 127131 127133 127137 127139 127143 127145 127147 127148 127149 127151 127152 127153 127155 127157 127161 127163 127167 127169 127173 127179 127181 127187 127191 127193 127197 127203 127209 127211 127217 127221 127223 127229 127233 127239 127247 366461
科目:
来源:第2章《二次函数》中考题集(28):2.3 二次函数的应用(解析版)
题型:解答题
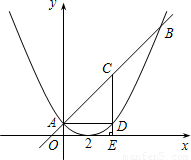
如图,已知二次函数图象的顶点坐标为(2,0),直线y=x+1与二次函数的图象交于A,B两点,其中点A在y轴上.
(1)二次函数的解析式为y=______;
(2)证明:点(-m,2m-1)不在(1)中所求的二次函数的图象上;
(3)若C为线段AB的中点,过C点作CE⊥x轴于E点,CE与二次函数的图象交于D点.
①y轴上存在点K,使以K,A,D,C为顶点的四边形是平行四边形,则K点的坐标是______;
②二次函数的图象上是否存在点p,使得S
三角形POE=2S
三角形ABD?求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(28):2.3 二次函数的应用(解析版)
题型:解答题
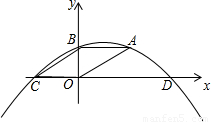
如图,四边形ABCO是平行四边形,AB=4,OB=2,抛物线过A、B、C三点,与x轴交于另一点D.一动点P以每秒1个单位长度的速度从B点出发沿BA向点A运动,运动到A停止,同时一动点Q从点D出发,以每秒3个单位长度的速度沿DC向点C运动,与点P同时停止.
(1)求抛物线的解析式;
(2)若抛物线的对称轴与AB交于点E,与x轴交于点F,当点P运动时间t为何值时,四边形POQE是等腰梯形?
(3)当t为何值时,以P、B、O为顶点的三角形与以点Q、B、O为顶点的三角形相似?
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(28):2.3 二次函数的应用(解析版)
题型:解答题

如图,已知抛物线y=ax
2-4x+c经过点A(0,-6)和B(3,-9).
(1)求出抛物线的解析式;
(2)写出抛物线的对称轴方程及顶点坐标;
(3)点P(m,m)与点Q均在抛物线上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q的坐标;
(4)在满足(3)的情况下,在抛物线的对称轴上寻找一点M,使得△QMA的周长最小.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(28):2.3 二次函数的应用(解析版)
题型:解答题
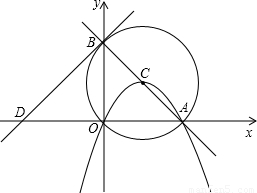
如图,直线y=-x+6与x轴交于点A,与y轴交于点B,以线段AB为直径作⊙C,抛物线y=ax
2+bx+c过A、C、O三点.
(1)求点C的坐标和抛物线的解析式;
(2)过点B作直线与x轴交于点D,且OB
2=OA•OD,求证:DB是⊙C的切线;
(3)抛物线上是否存在一点P,使以P、O、C、A为顶点的四边形为直角梯形?如果存在,求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(28):2.3 二次函数的应用(解析版)
题型:解答题
在平面直角坐标系中,点O是坐标原点,点P(m,-1)(m>0).连接OP,将线段OP绕点O按逆时针方向旋转90°得到线段OM,且点M是抛物线y=ax2+bx+c的顶点.
(1)若m=1,抛物线y=ax2+bx+c经过点(2,2),当0≤x≤1时,求y的取值范围;
(2)已知点A(1,0),若抛物线y=ax2+bx+c与y轴交于点B,直线AB与抛物线y=ax2+bx+c有且只有一个交点,请判断△BOM的形状,并说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(28):2.3 二次函数的应用(解析版)
题型:解答题
如图,抛物线y
1=ax
2-2ax+b经过A(-1,0),C(0,

)两点,与x轴交于另一点B.
(1)求此抛物线的解析式;
(2)若抛物线的顶点为M,点P为线段OB上一动点(不与点B重合),点Q在线段MB上移动,且∠MPQ=45°,设线段OP=x,MQ=
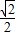
y
2,求y
2与x的函数关系式,并直接写出自变量x的取值范围;
(3)在同一平面直角坐标系中,两条直线x=m,x=n分别与抛物线交于点E、G,与(2)中的函数图象交于点F、H.问四边形EFHG能否成为平行四边形?若能,求m、n之间的数量关系;若不能,请说明理由.

查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(28):2.3 二次函数的应用(解析版)
题型:解答题
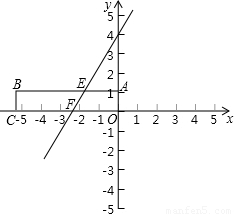
如图,在平面直角坐标系中放置一矩形ABCO,其顶点为A(0,1)、B(-3
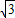
,1)、C(-3
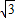
,0)、O(0,0).将此矩形沿着过E(-

,1)、F(-

,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′.
(1)求折痕所在直线EF的解析式;
(2)一抛物线经过B、E、B′三点,求此二次函数解析式;
(3)能否在直线EF上求一点P,使得△PBC周长最小?如能,求出点P的坐标;若不能,说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(28):2.3 二次函数的应用(解析版)
题型:解答题
如图,矩形ABCD的顶点A、B的坐标分别为(-4,0)和(2,0),BC=
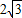
.设直线AC与直线x=4交于点E.
(1)求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E;
(2)设(1)中的抛物线与x轴的另一个交点为N,M是该抛物线上位于C、N之间的一动点,求△CMN面积的最大值.

查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(28):2.3 二次函数的应用(解析版)
题型:解答题
已知二次函数y=ax2+bx+c(a≠0)的图象经过O(0,0),M(1,1)和N(n,0)
(n≠0)三点.
(1)若该函数图象顶点恰为M点,写出此时n的值及y的最大值;
(2)当n=-2时,确定这个二次函数的解析式,并判断此时y是否有最大值;
(3)由(1)、(2)可知,n的取值变化,会影响该函数图象的开口方向.请求出n满足什么条件时,y有最小值.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(28):2.3 二次函数的应用(解析版)
题型:解答题
如图,抛物线y=ax
2+bx经过点A(4,0),B(2,2).连接OB,AB.
(1)求该抛物线的解析式;
(2)求证:△OAB是等腰直角三角形;
(3)将△OAB绕点O按顺时针方向旋转135°得到△OA′B′,写出△OA′B′的边A′B′的中点P的坐标.试判断点P是否在此抛物线上,并说明理由.

查看答案和解析>>



 如图,已知抛物线y=ax2-4x+c经过点A(0,-6)和B(3,-9).
如图,已知抛物线y=ax2-4x+c经过点A(0,-6)和B(3,-9).
 )两点,与x轴交于另一点B.
)两点,与x轴交于另一点B.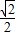 y2,求y2与x的函数关系式,并直接写出自变量x的取值范围;
y2,求y2与x的函数关系式,并直接写出自变量x的取值范围;
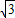 ,1)、C(-3
,1)、C(-3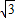 ,0)、O(0,0).将此矩形沿着过E(-
,0)、O(0,0).将此矩形沿着过E(- ,1)、F(-
,1)、F(- ,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′.
,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′.
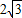 .设直线AC与直线x=4交于点E.
.设直线AC与直线x=4交于点E.
