
科目: 来源:第2章《二次函数》中考题集(25):2.3 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(25):2.3 二次函数的应用(解析版) 题型:解答题
| 行驶速度(千米/时) | 40 | 60 | 80 | … |
| 停止距离(米) | 16 | 30 | 48 | … |
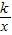 (k≠0);③y=ax2+bx,请选择恰当的函数来描述停止距离y(米)与汽车行驶速度x(千米/时)的关系,说明选择理由,并求出符合要求的函数的解析式;
(k≠0);③y=ax2+bx,请选择恰当的函数来描述停止距离y(米)与汽车行驶速度x(千米/时)的关系,说明选择理由,并求出符合要求的函数的解析式;查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(25):2.3 二次函数的应用(解析版) 题型:解答题
 取2.2,结果精确到0.1m).
取2.2,结果精确到0.1m).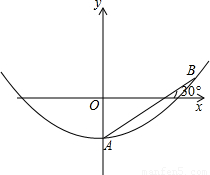
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(25):2.3 二次函数的应用(解析版) 题型:解答题
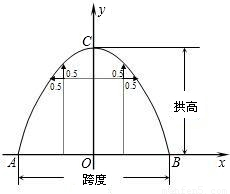
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(25):2.3 二次函数的应用(解析版) 题型:解答题
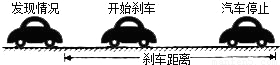
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(25):2.3 二次函数的应用(解析版) 题型:解答题
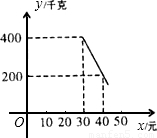
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(25):2.3 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(25):2.3 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(25):2.3 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(25):2.3 二次函数的应用(解析版) 题型:解答题
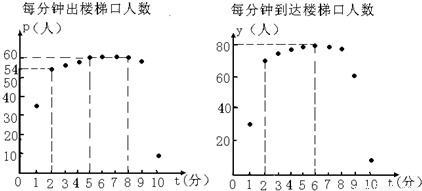
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com