
科目: 来源:第1章《反比例函数》中考题集(26):1.3 实际生活中的反比例函数(解析版) 题型:解答题
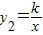 (x<0)分别交于点C、D,且C点的坐标为(-1,2).
(x<0)分别交于点C、D,且C点的坐标为(-1,2).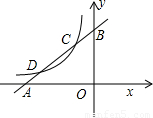
查看答案和解析>>
科目: 来源:第1章《反比例函数》中考题集(26):1.3 实际生活中的反比例函数(解析版) 题型:解答题
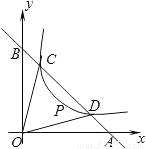
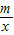 在第一象限分支上的两点,直线CD分别交x轴、y轴于A、B两点.设C(x1,y1)、D(x2,y2),连接OC、OD(O是坐标有点),若∠BOC=∠AOD=α,且tanα=
在第一象限分支上的两点,直线CD分别交x轴、y轴于A、B两点.设C(x1,y1)、D(x2,y2),连接OC、OD(O是坐标有点),若∠BOC=∠AOD=α,且tanα= ,OC=
,OC= .
.
查看答案和解析>>
科目: 来源:第1章《反比例函数》中考题集(26):1.3 实际生活中的反比例函数(解析版) 题型:解答题
 )处,两直角边分别与
)处,两直角边分别与 x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+ 与双曲线y=
与双曲线y=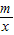 (m>0)的交点.
(m>0)的交点.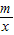 (m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN=
(m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN= AB,写出你的探究过程和结论.
AB,写出你的探究过程和结论.查看答案和解析>>
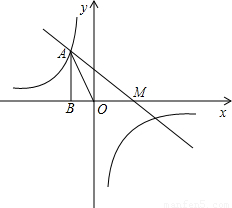
科目: 来源:第1章《反比例函数》中考题集(26):1.3 实际生活中的反比例函数(解析版) 题型:解答题
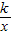 的图象经过点A(-
的图象经过点A(-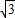 ,b),过点A作AB⊥x轴,垂足为点B,△AOB的面积为
,b),过点A作AB⊥x轴,垂足为点B,△AOB的面积为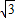 .
.
查看答案和解析>>
科目: 来源:第1章《反比例函数》中考题集(26):1.3 实际生活中的反比例函数(解析版) 题型:解答题
 有两个不同的公共点A、B.
有两个不同的公共点A、B.查看答案和解析>>
科目: 来源:第1章《反比例函数》中考题集(26):1.3 实际生活中的反比例函数(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第1章《反比例函数》中考题集(26):1.3 实际生活中的反比例函数(解析版) 题型:解答题
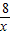 与一次函数y=-x+2的图象交于A、B两点.
与一次函数y=-x+2的图象交于A、B两点.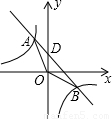
查看答案和解析>>
科目: 来源:第1章《反比例函数》中考题集(26):1.3 实际生活中的反比例函数(解析版) 题型:解答题
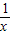 的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: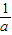 )、R(b,
)、R(b,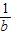 ),求直线OM对应的函数表达式(用含a,b的代数式表示);
),求直线OM对应的函数表达式(用含a,b的代数式表示); ∠AOB;
∠AOB;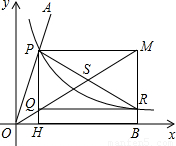
查看答案和解析>>
科目: 来源:第1章《反比例函数》中考题集(26):1.3 实际生活中的反比例函数(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第1章《反比例函数》中考题集(26):1.3 实际生活中的反比例函数(解析版) 题型:解答题
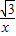 的图象上,求点C的坐标.
的图象上,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com