相关习题
0 127186 127194 127200 127204 127210 127212 127216 127222 127224 127230 127236 127240 127242 127246 127252 127254 127260 127264 127266 127270 127272 127276 127278 127280 127281 127282 127284 127285 127286 127288 127290 127294 127296 127300 127302 127306 127312 127314 127320 127324 127326 127330 127336 127342 127344 127350 127354 127356 127362 127366 127372 127380 366461
科目:
来源:第1章《反比例函数》中考题集(21):1.3 实际生活中的反比例函数(解析版)
题型:填空题
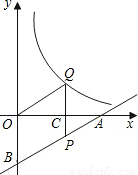
如图,一次函数y=

x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数

(k>0)的图象于Q,S
△OQC=

,则k的值和Q点的坐标分别为k=
,Q
.
查看答案和解析>>
科目:
来源:第1章《反比例函数》中考题集(23):1.3 实际生活中的反比例函数(解析版)
题型:解答题
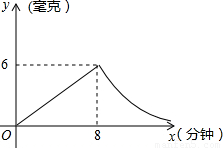
为预防“流感“,某单位对办公室进行“药熏消毒”.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物8分钟燃毕,此时办公室内每立方米空气中含药量为6毫克,据以上信息:
(1)分别求药物燃烧时和燃烧后,y与x的函数关系式;
(2)研究表明,当空气中含药量低于1.6毫克/立方米时,工作人员才能回到办公室,那么从消毒开始,经多长时间,工作人员才可以回到办公室?
查看答案和解析>>
科目:
来源:第1章《反比例函数》中考题集(23):1.3 实际生活中的反比例函数(解析版)
题型:解答题
某市城建部门经过长期市场调查发现,该市年新建商品房面积P(万平方米)与市场新房均价x(千元/平方米)存在函数关系P=25x;年新房销售面积Q(万平方米)与市场新房均价x(千元/平方米)的函数关系为
Q=

-10;
(1)如果年新建商品房的面积与年新房销售面积相等,求市场新房均价和年新房销售总额;
(2)在(1)的基础上,如果市场新房均价上涨1千元,那么该市年新房销售总额是增加还是减少?变化了多少?结合年新房销售总额和积压面积的变化情况,请你提出一条合理化的建议.(字数不超过50)
查看答案和解析>>
科目:
来源:第1章《反比例函数》中考题集(23):1.3 实际生活中的反比例函数(解析版)
题型:解答题
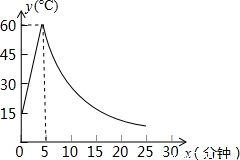
制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:
来源:第1章《反比例函数》中考题集(23):1.3 实际生活中的反比例函数(解析版)
题型:解答题
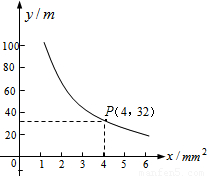
你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)s(mm
2)的反比例函数,其图象如图所示.
(1)写出y与s的函数关系式;
(2)求当面条粗1.6mm
2时,面条的总长度是多少米?
查看答案和解析>>
科目:
来源:第1章《反比例函数》中考题集(23):1.3 实际生活中的反比例函数(解析版)
题型:解答题
某小型开关厂今年准备投入一定的经费用于现有生产设备的改造以提高经济效益.通过测算:今年开关的年产量y(万只)与投入的改造经费x(万元)之间满足3-y与x+1成反比例,且当改造经费投入1万元时,今年的年产量是2万只.
(1)求年产量y(万只)与改造经费x(万元)之间的函数解析式.(不要求写出x的取值范围)
(2)已知每生产1万只开关所需要的材料费是8万元.除材料费外,今年在生产中,全年还需支付出2万元的固定费用.
①求平均每只开关所需的生产费用为多少元?(用含y的代数式表示)
(生产费用=固定费用+材料费)
②如果将每只开关的销售价定位“平均每只开关的生产费用的1.5倍”与“平均每只开关所占改造费用的一半”之和,那么今年生产的开关正好销完.问今年需投入多少改造经费,才能使今年的销售利润为9.5万元?
(销售利润=销售收入一生产费用-改造费用)
查看答案和解析>>
科目:
来源:第1章《反比例函数》中考题集(23):1.3 实际生活中的反比例函数(解析版)
题型:解答题
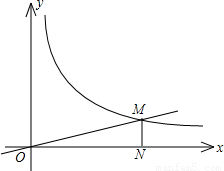
已知:正比例函数y=k
1x的图象与反比例函数

(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式.
查看答案和解析>>
科目:
来源:第1章《反比例函数》中考题集(23):1.3 实际生活中的反比例函数(解析版)
题型:解答题
已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S
△AOB=4.
(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.

查看答案和解析>>
科目:
来源:第1章《反比例函数》中考题集(23):1.3 实际生活中的反比例函数(解析版)
题型:解答题
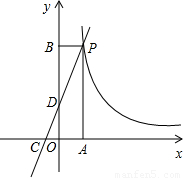
如图,一次函数y=kx+2的图象与反比例函数y=
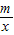
的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交x轴、y轴于点C、D,且S
△PBD=4,

=

.
(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当x>0时,一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:
来源:第1章《反比例函数》中考题集(23):1.3 实际生活中的反比例函数(解析版)
题型:解答题
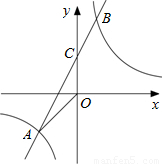
如图,已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=

的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)求不等式kx+b-
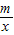
<0的解集.(直接写出答案)
查看答案和解析>>

 x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数
x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数 (k>0)的图象于Q,S△OQC=
(k>0)的图象于Q,S△OQC= ,则k的值和Q点的坐标分别为k= ,Q .
,则k的值和Q点的坐标分别为k= ,Q .

 -10;
-10;

 (x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式.
(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式.

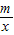 的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,
的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4, =
= .
.
 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.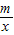 <0的解集.(直接写出答案)
<0的解集.(直接写出答案)