
科目: 来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
 米,试求AD的长度.(结果带根号)
米,试求AD的长度.(结果带根号)
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
 .
. 米).
米).查看答案和解析>>
科目: 来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
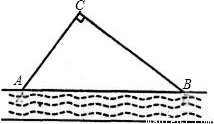
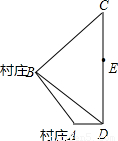 如图所示,A、B为两个村庄,AB、BC、CD为公路,BD为田地,AD为河宽,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一条电缆,共有如下两种铺设方案:
如图所示,A、B为两个村庄,AB、BC、CD为公路,BD为田地,AD为河宽,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一条电缆,共有如下两种铺设方案: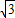 千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15度.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.
千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15度.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.查看答案和解析>>
科目: 来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
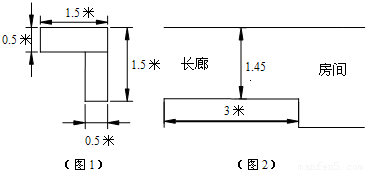
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
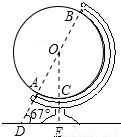
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》常考题集(19):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
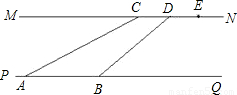
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》常考题集(19):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
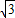 ,∠ABC=30°,tan30°=
,∠ABC=30°,tan30°= =
=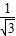 =
=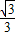 ,在此图的基础上通过添加适当的辅助线,可求出tan15°的值.请你写出添加辅助线的方法,并求出tan15°的值.
,在此图的基础上通过添加适当的辅助线,可求出tan15°的值.请你写出添加辅助线的方法,并求出tan15°的值.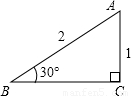
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com