相关习题
0 127258 127266 127272 127276 127282 127284 127288 127294 127296 127302 127308 127312 127314 127318 127324 127326 127332 127336 127338 127342 127344 127348 127350 127352 127353 127354 127356 127357 127358 127360 127362 127366 127368 127372 127374 127378 127384 127386 127392 127396 127398 127402 127408 127414 127416 127422 127426 127428 127434 127438 127444 127452 366461
科目:
来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版)
题型:填空题
王英同学从A地沿北偏西60°方向走100米到B地,再从B地向正南方向走200米到C地,此时王英同学离A地的距离是 米.
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版)
题型:填空题
小明骑自行车以15千米/小时的速度在公路上向正北方向匀速行进,如图,出发时,在B点他观察到仓库A在他的北偏东30°处,骑行20分钟后到达C点,发现此时这座仓库正好在他的东南方向,则这座仓库到公路的距离为
千米.(参考数据:
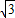
≈1.732,结果保留两位有效数字)
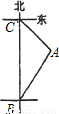
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版)
题型:填空题
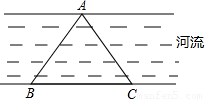
如图,B、C是洲河岸边两点,A是河对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=200米,则点A到岸边BC的距离是
米.
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版)
题型:填空题
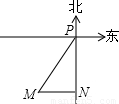
如图,一艘轮船向正东方向航行,上午9时测得它在灯塔P的南偏西30°方向、距离灯塔120海里的M处,上午11时到达这座灯塔的正南方向的N处,则这艘轮船在这段时间内航行的平均速度是
海里/小时.
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版)
题型:填空题
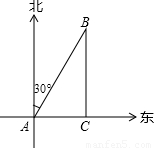
一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A处测得某灯塔位于它的北偏东30°的B处,如图所示,上午9时行至C处,测得灯塔恰好在它的正北方向,此时它与灯塔的距离是
海里(结果保留根号).
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版)
题型:填空题
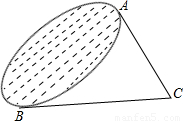
如图,为了求出湖两岸A、B两点之间的距离,观测者在湖边找到一点C,并分别测∠BAC=90°,∠ABC=30°,又量得BC=160m,则A、B两点之间距离为
m(结果保留根号).
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
如图1,一扇窗户打开后用窗钩AB可将其固定.
(1)这里所运用的几何原理是( )
(A)三角形的稳定性(B)两点之间线段最短;
(C)两点确定一条直线(D)垂线段最短;
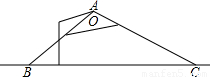
(2)图2是图1中窗子开到一定位置时的平面图,若∠AOB=45°,∠OAB=30°,OA=60cm,求点B到OA边的距离.(
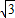
≈1.7,结果精确到整数)
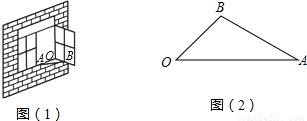
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
如图,一盏路灯沿灯罩边缘射出的光线与地面BC交于点B、C,测得∠ABC=45°,∠ACB=30°,且BC=20米.
(1)请用圆规和直尺画出路灯A到地面BC的距离AD;(不要求写出画法,但要保留作图痕迹)
(2)求出路灯A离地面的高度AD.(精确到0.1米)(参考数据:
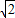
≈1.414,
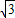
≈1.732).
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
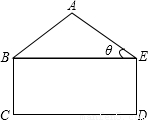
某工厂接受一批支援四川省汶川灾区抗震救灾帐篷的生产任务.根据要求,帐篷的一个横截面框架由等腰三角形和矩形组成(如图所示).已知等腰△ABE的底角∠AEB=θ,且tanθ=

,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m,求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》常考题集(17):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
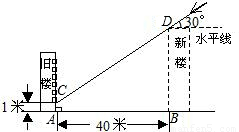
为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?
查看答案和解析>>

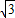 ≈1.732,结果保留两位有效数字)
≈1.732,结果保留两位有效数字)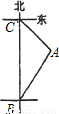




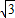 ≈1.7,结果精确到整数)
≈1.7,结果精确到整数)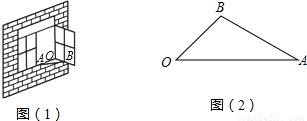
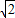 ≈1.414,
≈1.414,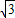 ≈1.732).
≈1.732).
 ,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m,求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m,求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
