
科目: 来源:第7章《锐角三角函数》中考题集(45):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
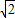 ≈1.414,
≈1.414,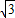 ≈1.732)
≈1.732)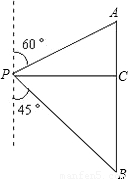
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(45):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
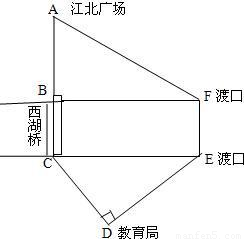
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(45):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
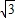 ≈1.732,
≈1.732,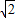 ≈1.414)
≈1.414)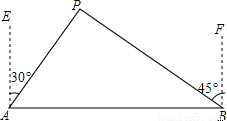
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(45):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
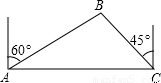
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(45):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
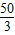 米/秒),并在离该公路100米处设置了一个监测点A.在如图所示的直角坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在A的北偏西60°方向上,点C在A的北偏东45°方向上,另外一条高等级公路在y轴上,AO为其中的一段.
米/秒),并在离该公路100米处设置了一个监测点A.在如图所示的直角坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在A的北偏西60°方向上,点C在A的北偏东45°方向上,另外一条高等级公路在y轴上,AO为其中的一段.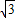 ≈1.7)
≈1.7)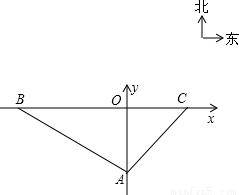
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(45):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
 ≈1.732)
≈1.732)
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(45):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
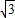 ≈1.73,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
≈1.73,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)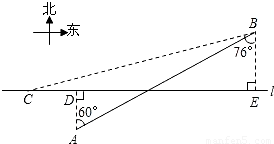
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(45):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
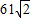 千米,且位于临海市(记作点B)正西方向
千米,且位于临海市(记作点B)正西方向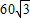 千米处,台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.
千米处,台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.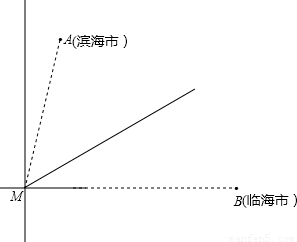
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(45):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
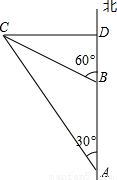
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(45):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
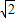 ≈1.4,
≈1.4,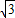 ≈1.7,结果保留整数).
≈1.7,结果保留整数).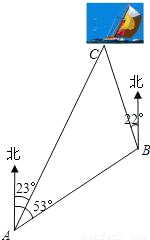
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com