
科目: 来源:第7章《锐角三角函数》中考题集(43):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
 =1.414,
=1.414, =1.732)
=1.732)
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(43):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
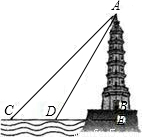
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(43):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
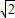 ,7+
,7+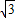 时,求代数式
时,求代数式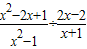 的值.小明一看,“太复杂了,怎么算呢?”你能帮小明解决这个问题吗?请你写出具体过程;
的值.小明一看,“太复杂了,怎么算呢?”你能帮小明解决这个问题吗?请你写出具体过程;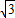 ≈1.7)
≈1.7)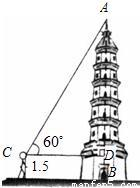
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(43):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
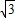 =1.73)
=1.73)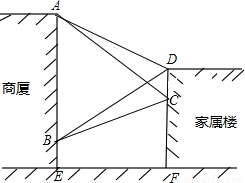
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(43):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
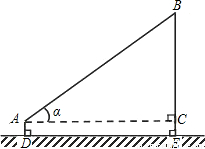
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(43):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
| 题目 | 测量底部可以达到的铁塔的高 | |
| 组别 | 甲组 | 乙组 |
| 测 量 目 标 | 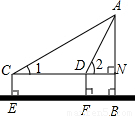 |  |
| 测量 数据 | ∠1=30°∠2=60° EF=30m CE=DF=NB=1.3m | ∠α=27°27′ BP=50m MP=NB=1.3m |
| 计 算 | 选择______组测量方案 | |
| 参考 数据 | 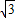 ≈1.732 ≈1.732 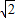 ≈1,414 sin27°27′≈0.416 ≈1,414 sin27°27′≈0.416 cos27°27′≈0.887 tan27°27′≈0.520 cot27°27′≈1.925 | |
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(43):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
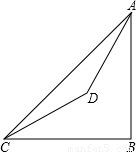
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(43):7.6 锐角三角函数的简单应用(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(43):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
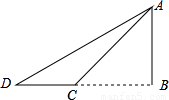
查看答案和解析>>
科目: 来源:第7章《锐角三角函数》中考题集(43):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
 (即tan∠PAB=
(即tan∠PAB= ),且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
),且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)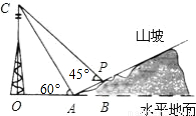
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com