相关习题
0 127317 127325 127331 127335 127341 127343 127347 127353 127355 127361 127367 127371 127373 127377 127383 127385 127391 127395 127397 127401 127403 127407 127409 127411 127412 127413 127415 127416 127417 127419 127421 127425 127427 127431 127433 127437 127443 127445 127451 127455 127457 127461 127467 127473 127475 127481 127485 127487 127493 127497 127503 127511 366461
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
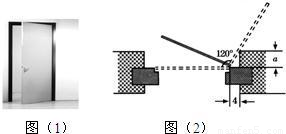
图(1)是一扇半开着的办公室门的照片,门框镶嵌在墙体中间,门是向室内开的.图(2)画的是它的一个横断面.虚线表示门完全关好和开到最大限度(由于受到墙角的阻碍,再也开不动了)时的两种情形,这时二者的夹角为120°,从室内看门框露在外面部分的宽为4cm,求室内露出的墙的厚度a的值.(假设该门无论开到什么角度,门和门框之间基本都是无缝的.精确到0.1cm,
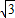
≈1.73)
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
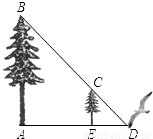
如图,小鸟的妈妈在地面D处寻找到食物,准备飞到大树的顶端B处给非常饥饿的小鸟喂食,途中经过小树树顶C处,已知小树高为4米,大树与小树之间的距离为9米,已知tan∠BDA=

,问小鸟妈妈从D处飞到B处至少要飞行多少米?(D、C、B三点共线)
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
某工厂接受一批支援四川省汶川灾区抗震救灾帐篷的生产任务.根据要求,帐篷的一个横截面框架由等腰三角形和矩形组成(如图所示).已知等腰△ABE的底角∠AEB=θ,且tanθ=

,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m,求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)

查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
如图,救援人员在地平面的A点,用生命探测仪测得正下方B点有生命迹象,救援队在与A点同一水平面外的C点沿着CB方向挖掘,已知∠ACB=30°,AC=
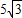
米,若挖掘的速度为2米/小时,几小时后到达B点?
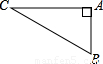
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
在一次课题学习课上,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2米,BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18.6°,最大夹角β为64.5度.请你根据以上数据,帮助小明同学计算出遮阳蓬中CD的长是多少米?(结果保留两个有效数字)
(参考数据:sin18.6°=0.32,tan18.6°=0.34,sin64.5°=0.90,tan64.5°=2.1)

查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?
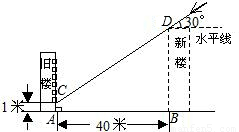
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
曙光中学需制作一副简易篮球架,如图是篮球架的侧面示意图,已知篮板所在直线AD和直杆EC都与BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜杆AB与直杆EC的长分别是多少米?(结果精确到0.01米)
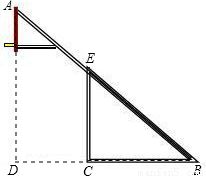
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
要挖掘地下文物,需测出文物离地面的距离.如图,考古队在文物上方地面A处用仪器测文物C,探测线与地面夹角为30°,在沿文物方向前进20米的B处,又测得探测线与地面夹角为60°,求文物C到地面的距离.
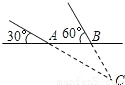
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
如图所示,张伯伯利用假日在某钓鱼场钓鱼,风平浪静时,鱼漂露出水面部分AB=6cm,微风吹来,假设铅垂P不动,鱼漂移动了一段距离BC,且顶端恰好与水面齐平,(即PA=PC)水平l与OC的夹角α为8°(点A在OC上),求铅锤P处的水深h.
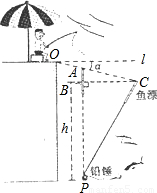
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
如图,两幢楼高AB=CD=30m,两楼间的距离AC=24m,当太阳光线与水平线的夹角为30°时,求甲楼投在乙楼上的影子的高度.(结果精确到0.01,
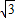
≈1.732,
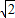
≈1.414)
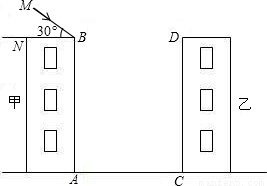
查看答案和解析>>

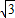 ≈1.73)
≈1.73)
 ,问小鸟妈妈从D处飞到B处至少要飞行多少米?(D、C、B三点共线)
,问小鸟妈妈从D处飞到B处至少要飞行多少米?(D、C、B三点共线)
 ,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m,求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m,求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
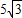 米,若挖掘的速度为2米/小时,几小时后到达B点?
米,若挖掘的速度为2米/小时,几小时后到达B点?





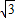 ≈1.732,
≈1.732,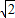 ≈1.414)
≈1.414)