相关习题
0 127319 127327 127333 127337 127343 127345 127349 127355 127357 127363 127369 127373 127375 127379 127385 127387 127393 127397 127399 127403 127405 127409 127411 127413 127414 127415 127417 127418 127419 127421 127423 127427 127429 127433 127435 127439 127445 127447 127453 127457 127459 127463 127469 127475 127477 127483 127487 127489 127495 127499 127505 127513 366461
科目:
来源:第7章《锐角三角函数》中考题集(34):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
某厂房屋顶呈人字架形(等腰三角形),如图所示,已知AC=BC=8m,∠A=30°,CD⊥AB于点D.
(1)求∠ACB的大小;
(2)求AB的长度.

查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(34):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
(1)判断AB,AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).
(参考数据:
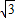
≈1.73,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)

查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(34):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
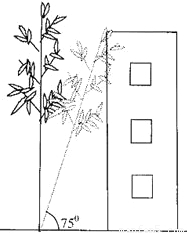
如图,一幢楼房前有一棵竹子,楼底到竹子的距离CB为2米,阵风吹过,竹子的顶端恰好到达楼顶,此时测得竹子与水平地面的夹角为75°,求这棵竹子比楼房高出多少米?(精确到0.1米)
(参考数据:sin75°=0.996,cos75°=0.259,tan75°=3.732)
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(34):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
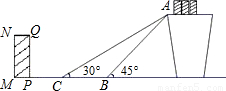
如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:(1)(2)的计算结果精确到0.1米,参考数据:

≈1.41,
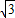
≈1.73,
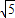
≈2.24,
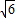
≈2.45)
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
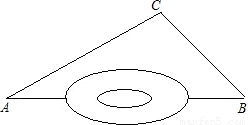
如图,A、B两地被一大山阻隔,汽车从A地到B须经过C地中转.为了促进A、B两地的经济发展,现计划开通隧道,使汽车可以直接从A地到B地.已知∠A=30°,∠B=45°,BC=

千米.若汽车的平均速度为45千米/时,则隧道开通后,汽车直接从A地到B地需要多长时间?(参考数据:
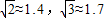
)
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
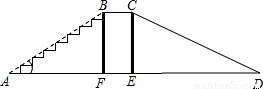
某公园有一滑梯,横截面如图所示,AB表示楼梯,BC表示平台,CD表示滑道.若点E,F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=

,BF=3米,BC=1米,CD=6米.
求:(1)∠D的度数;
(2)线段AE的长.
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
某商场为缓解我市“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说的对?请你判断并计算出正确的结果.(参考数据:sin18°=0.31,cos18°=0.95,tan18°=0.325)
(结果精确到0.1m)

查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
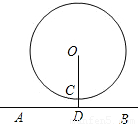
如图,是一个匀速旋转(指每分钟旋转的弧长或圆心角相同)的摩天轮的示意图,O为圆心,AB为水平地面,假设摩天轮的直径为80米,最低点C离地面为6米,旋转一周所用的时间为6分钟,小明从点C乘坐摩天轮(身高忽略不计),请问:
(1)经过2分钟后,小明离开地面的高度大约是多少米?
(2)若小明到了最高点,在视线没有阻挡的情况下能看到周围3公里远的地面景物,则他看到的地面景物有多大面积?(精确到1平方公里)
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此太阳光线与地面成30°夹角.(

1.4,
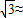
1.7)
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了
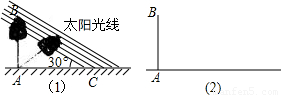
变化,假设太阳光线于地面夹角保持不变(用图(2)解答)
①求树与地面成45°角时的影长;
②求树的最大影长.
查看答案和解析>>
科目:
来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
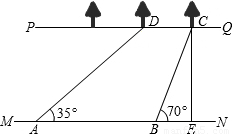
如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测得∠DAN=35°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CE(结果保留两个有效数字).
(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>


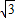 ≈1.73,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)
≈1.73,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)

 ≈1.41,
≈1.41,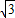 ≈1.73,
≈1.73,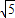 ≈2.24,
≈2.24,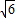 ≈2.45)
≈2.45)
 千米.若汽车的平均速度为45千米/时,则隧道开通后,汽车直接从A地到B地需要多长时间?(参考数据:
千米.若汽车的平均速度为45千米/时,则隧道开通后,汽车直接从A地到B地需要多长时间?(参考数据: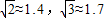 )
)
 ,BF=3米,BC=1米,CD=6米.
,BF=3米,BC=1米,CD=6米.


 1.4,
1.4,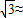 1.7)
1.7) 变化,假设太阳光线于地面夹角保持不变(用图(2)解答)
变化,假设太阳光线于地面夹角保持不变(用图(2)解答)