相关习题
0 127413 127421 127427 127431 127437 127439 127443 127449 127451 127457 127463 127467 127469 127473 127479 127481 127487 127491 127493 127497 127499 127503 127505 127507 127508 127509 127511 127512 127513 127515 127517 127521 127523 127527 127529 127533 127539 127541 127547 127551 127553 127557 127563 127569 127571 127577 127581 127583 127589 127593 127599 127607 366461
科目:
来源:第6章《二次函数》常考题集(26):6.4 二次函数的应用(解析版)
题型:解答题
如图,抛物线y=x
2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S
△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(26):6.4 二次函数的应用(解析版)
题型:解答题
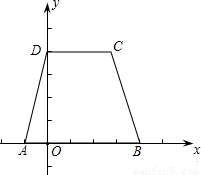
如图,在平面直角坐标系中,已知四边形ABCD是等腰梯形,A、B在x轴上,D在y轴上,AB∥CD,AD=BC=
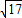
,AB=5,CD=3,抛物线y=-x
2+bx+c过A、B两点.
(1)求b、c;
(2)设M是x轴上方抛物线上的一动点,它到x轴与y轴的距离之和为d,求d的最大值;
(3)当(2)中M点运动到使d取最大值时,此时记点M为N,设线段AC与y轴交于点E,F为线段EC上一动点,求F到N点与到y轴的距离之和的最小值,并求此时F点的坐标.
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(26):6.4 二次函数的应用(解析版)
题型:解答题
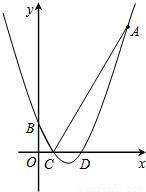
如图,抛物线的顶点坐标是
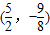
,且经过点A(8,14).
(1)求该抛物线的解析式;
(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;
(3)设点P是x轴上的任意一点,分别连接AC、BC.试判断:PA+PB与AC+BC的大小关系,并说明理由.
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(26):6.4 二次函数的应用(解析版)
题型:解答题
已知抛物线y=x2+(n-3)x+n+1经过坐标原点O.
(1)求这条抛物线的顶点P的坐标;
(2)设这条抛物线与x轴的另一个交点为A,求以直线PA为图象的一次函数解析式.
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(26):6.4 二次函数的应用(解析版)
题型:解答题
如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动.当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
(1)求P点从A点运动到D点所需的时间;
(2)设P点运动时间为t(秒).
①当t=5时,求出点P的坐标;
②若△OAP的面积为s,试求出s与t之间的函数关系式(并写出相应的自变量t的取值范围).
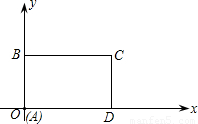
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(26):6.4 二次函数的应用(解析版)
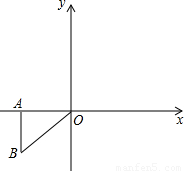
题型:解答题
如图,△ABO中,O是坐标原点,A
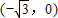
,B
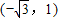
.
(1)①以原点O为位似中心,将△ABO放大,使变换后得到的△CDO与△ABO的位似比为2:1,且D在第一象限内,则C点坐标为(______
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(26):6.4 二次函数的应用(解析版)
题型:解答题
如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么
(1)设△POQ的面积为y,求y关于t的函数解析式;
(2)当△POQ的面积最大时,将△POQ沿直线PQ翻折后得到△PCQ,试判断点C是否落在直线AB上,并说明理由;
(3)当t为何值时,△POQ与△AOB相似.
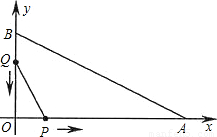
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(26):6.4 二次函数的应用(解析版)
题型:解答题
如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点,若抛物线y=ax
2+bx+4经过A,B,C三点,且AB=6.
(1)求⊙P的半径R的长;
(2)求该抛物线的解析式并直接写出该抛物线与⊙P的第四个交点E的坐标;
(3)若以AB为直径的圆与直线AC的交点为F,求AF的长.

查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(26):6.4 二次函数的应用(解析版)
题型:解答题
如图,直线y=-x+3与x轴、y轴分别交于点B、C,抛物线y=-x
2+bx+c经过点B、C,点A是抛物线与x轴的另一个交点.
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)若P是抛物线上一点,且S
△ABP=

S
△ABC,这样的点P有______个.

查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(26):6.4 二次函数的应用(解析版)
题型:解答题
如图,在平面直角坐标系中,两个一次函数y=x,y=-2x+12的图象相交于点A,动点E从O点出发,沿OA方向以每秒1个单位的速度运动,作EF∥y轴与直线BC交于点F,以EF为一边向x轴负方向作正方形EFMN,设正方形EFMN与△AOC的重叠部分的面积为S.
(1)求点A的坐标;
(2)求过A、B、O三点的抛物线的顶点P的坐标;
(3)当点E在线段OA上运动时,求出S与运动时间t(秒)的函数表达式;
(4)在(3)的条件下,t为何值时,S有最大值,最大值是多少?此时(2)中的抛物线的顶点P是否在直线EF上,请说明理由.

查看答案和解析>>


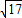 ,AB=5,CD=3,抛物线y=-x2+bx+c过A、B两点.
,AB=5,CD=3,抛物线y=-x2+bx+c过A、B两点.
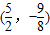 ,且经过点A(8,14).
,且经过点A(8,14).

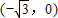 ,B
,B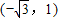 .
.


 S△ABC,这样的点P有______个.
S△ABC,这样的点P有______个.
