相关习题
0 127417 127425 127431 127435 127441 127443 127447 127453 127455 127461 127467 127471 127473 127477 127483 127485 127491 127495 127497 127501 127503 127507 127509 127511 127512 127513 127515 127516 127517 127519 127521 127525 127527 127531 127533 127537 127543 127545 127551 127555 127557 127561 127567 127573 127575 127581 127585 127587 127593 127597 127603 127611 366461
科目:
来源:第6章《二次函数》常考题集(24):6.4 二次函数的应用(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c与y轴的交点为C,顶点为M,直线CM的解析式y=-x+2并且线段CM的长为

.
(1)求抛物线的解析式;
(2)设抛物线与x轴有两个交点A(x
1,0)、B(x
2,0),且点A在B的左侧,求线段AB的长;
(3)若以AB为直径作⊙N,请你判断直线CM与⊙N的位置关系,并说明理由.

查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(24):6.4 二次函数的应用(解析版)
题型:解答题
如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG.请探究:
(1)线段AE与CG是否相等请说明理由:
(2)若设AE=x,DH=y,当x取何值时,y最大?
(3)连接BH,当点E运动到AD的何位置时,△BEH∽△BAE?

查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(24):6.4 二次函数的应用(解析版)
题型:解答题
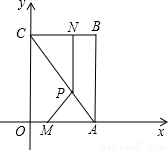
如图,在矩形ABCD中,AB=2AD,线段EF=10.在EF上取一点M,分别以EM、MF为一边作矩形EMNH、矩形MFGN,使矩形MFGN∽矩形ABCD.令MN=x,当x为何值时,矩形EMNH的面积S有最大值,最大值是多少?

查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(24):6.4 二次函数的应用(解析版)
题型:解答题
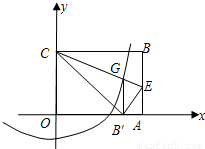
如图:在直角坐标系中放入一边长OC为6的矩形纸片ABCO,将纸翻折后,使点B恰好落在x轴上,记为B',折痕为CE,已知tan∠OB′C=

.
(1)求出B′点的坐标;
(2)求折痕CE所在直线的解析式;
(3)作B′G∥AB交CE于G,已知抛物线y=

x
2-

通过G点,以O为圆心OG的长为半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(24):6.4 二次函数的应用(解析版)
题型:解答题
如图,已知抛物线y=-

x
2+bx+c与坐标轴交于A,B,C三点,点A的横坐标为-1,过点C(0,3)的直线y=-
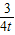
x+3与x轴交于点Q,点P是线段BC上的一个动点,PH⊥OB于点H.若PB=5t,且0<t<1.
(1)确定b,c的值;
(2)写出点B,Q,P的坐标(其中Q,P用含t的式子表示);
(3)依点P的变化,是否存在t的值,使△PQB为等腰三角形?若存在,求出所有t的值;若不存在,说明理由.

查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(24):6.4 二次函数的应用(解析版)
题型:解答题
如图1,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,D、E在x轴上,CF交y轴于点B(0,2),且其面积为8.
(1)求此抛物线的解析式;
(2)如图2,若P点为抛物线上不同于A的一点,连接PB并延长交抛物线于点Q,过点P、Q分别作x轴的垂线,垂足分别为S、R.
①求证:PB=PS;
②判断△SBR的形状;
③试探索在线段SR上是否存在点M,使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似?若存在,请找出M点的位置;若不存在,请说明理由.

查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(24):6.4 二次函数的应用(解析版)
题型:解答题
如图,在矩形ABCD中,AB=3cm,BC=4cm.设P,Q分别为BD,BC上的动点,在点P自点D沿DB方向作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P,Q移动的时间为t(0<t≤4).
(1)写出△PBQ的面积S(cm
2)与时间t(s)之间的函数表达式,当t为何值时,S有最大值,最大值是多少?
(2)当t为何值时,△PBQ为等腰三角形?
(3)△PBQ能否成为等边三角形?若能,求t的值;若不能,说明理由.

查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(25):6.4 二次函数的应用(解析版)
题型:解答题
如图,直线y=-x+3与x轴,y轴分别相交于点B,点C,经过B,C两点的抛物线y=ax
2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
(1)求A点的坐标;
(2)求该抛物线的函数表达式;
(3)连接AC.请问在x轴上是否存在点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(25):6.4 二次函数的应用(解析版)
题型:解答题
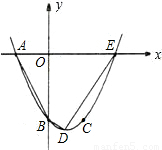
如图,已知抛物线y=ax
2+bx+c(a≠0)经过A(-2,0),B(0,-4),C(2,-4)三点,且与x轴的另一个交点为E.
(1)求抛物线的解析式;
(2)用配方法求抛物线的顶点D的坐标和对称轴;
(3)求四边形ABDE的面积.
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(25):6.4 二次函数的应用(解析版)
题型:解答题
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒.
(1)P点的坐标为多少;(用含x的代数式表示)
(2)试求△MPA面积的最大值,并求此时x的值;
(3)请你探索:当x为何值时,△MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果.
查看答案和解析>>

 .
.


 .
. x2-
x2- 通过G点,以O为圆心OG的长为半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
通过G点,以O为圆心OG的长为半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
 x2+bx+c与坐标轴交于A,B,C三点,点A的横坐标为-1,过点C(0,3)的直线y=-
x2+bx+c与坐标轴交于A,B,C三点,点A的横坐标为-1,过点C(0,3)的直线y=-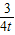 x+3与x轴交于点Q,点P是线段BC上的一个动点,PH⊥OB于点H.若PB=5t,且0<t<1.
x+3与x轴交于点Q,点P是线段BC上的一个动点,PH⊥OB于点H.若PB=5t,且0<t<1.




