
科目: 来源:第6章《二次函数》常考题集(17):6.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第6章《二次函数》常考题集(17):6.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第6章《二次函数》常考题集(17):6.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第6章《二次函数》常考题集(17):6.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第6章《二次函数》常考题集(17):6.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第6章《二次函数》常考题集(17):6.4 二次函数的应用(解析版) 题型:解答题
| 种植品种 数量 | A种作物 | B中作物 |
| 原种植量(棵) | 50 | 60 |
| 原产量(千克/棵) | 30 | 26 |
查看答案和解析>>
科目: 来源:第6章《二次函数》常考题集(17):6.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第6章《二次函数》常考题集(17):6.4 二次函数的应用(解析版) 题型:解答题
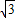 时x的值;
时x的值;
查看答案和解析>>
科目: 来源:第6章《二次函数》常考题集(17):6.4 二次函数的应用(解析版) 题型:解答题
 ,一年后发现实际每月的销售量p(台)与月次x之间存在如图所示的变化趋势.
,一年后发现实际每月的销售量p(台)与月次x之间存在如图所示的变化趋势.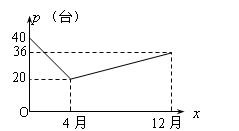
查看答案和解析>>
科目: 来源:第6章《二次函数》常考题集(17):6.4 二次函数的应用(解析版) 题型:解答题
 (x-8)2+12,1≤x≤11,且x为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少?
(x-8)2+12,1≤x≤11,且x为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com