相关习题
0 127438 127446 127452 127456 127462 127464 127468 127474 127476 127482 127488 127492 127494 127498 127504 127506 127512 127516 127518 127522 127524 127528 127530 127532 127533 127534 127536 127537 127538 127540 127542 127546 127548 127552 127554 127558 127564 127566 127572 127576 127578 127582 127588 127594 127596 127602 127606 127608 127614 127618 127624 127632 366461
科目:
来源:第6章《二次函数》常考题集(15):6.3 二次函数与一元二次方程(解析版)
题型:解答题
已知:二次函数y=x
2-2(m-1)x+m
2-2m-3,其中m为实数.
(1)求证:不论m取何实数,这个二次函数的图象与x轴必有两个交点;
(2)设这个二次函数的图象与x轴交于点A(x
1,0)、B(x
2,0),且x
1、x
2的倒数和为

,求这个二次函数的解析式.
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(15):6.3 二次函数与一元二次方程(解析版)
题型:解答题
已知:二次函数y=x
2-mx-4.
(1)求证:该函数的图象一定与x轴有两个不同的交点;
(2)设该函数的图象与x轴的交点坐标为(x
1,0)、(x
2,0),且

,求m的值,并求出该函数图象的顶点坐标.
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(15):6.3 二次函数与一元二次方程(解析版)
题型:解答题
一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).
(1)求此二次函数的解析式;
(2)用配方法求此抛物线的顶点为P;
(3)当x取什么值时,y随x增大而减小?
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(15):6.3 二次函数与一元二次方程(解析版)
题型:解答题
已知二次函数y=x2+bx+c的图象与x轴的两个交点的横坐标分别为x1、x2,一元二次方程x2+b2x+20=0的两实根为x3、x4,且x2-x3=x1-x4=3,求二次函数的解析式,并写出顶点坐标.
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(15):6.3 二次函数与一元二次方程(解析版)
题型:解答题
利用图象解一元二次方程x
2+x-3=0时,我们采用的一种方法是:在平面直角坐标系中画出抛物线y=x
2和直线y=-x+3,两图象交点的横坐标就是该方程的解.
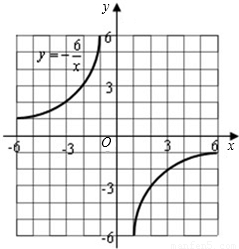
(1)填空:利用图象解一元二次方程x
2+x-3=0,也可以这样求解:在平面直角坐标系中画出抛物线y=______和直线y=-x,其交点的横坐标就是该方程的解.
(2)已知函数y=-
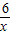
的图象(如图所示),利用图象求方程
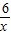
-x+3=0的近似解.(结果保留两个有效数字)
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(15):6.3 二次函数与一元二次方程(解析版)
题型:解答题
小明在复习数学知识时,针对“求一元二次方程的解”,整理了以下的几种方法,请你按有关内容补充完整:
| 复习日记卡片 |
| 内容:一元二次方程解法归纳 时间:2007年6月×日 |
| 举例:求一元二次方程x2-x-1=0的两个解 |
方法一:选择合适的一种方法(公式法、配方法、分解因式法)求解
解方程:x2-x-1=0.
解: |
方法二:利用二次函数图象与坐标轴的交点求解如图所示,把方程x2-x-1=0的解看成是二次函数y=______的图象与x轴交点的横坐标,即x1,x2就是方程的解.
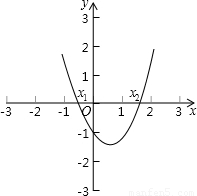 |
方法三:利用两个函数图象的交点求解
(1)把方程x2-x-1=0的解看成是一个二次函数y=______的图象与一个一次函数y=______图象交点的横坐标;
(2)画出这两个函数的图象,用x1,x2在x轴上标出方程的解.
 |
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(15):6.3 二次函数与一元二次方程(解析版)
题型:解答题
利用二次函数的图象求下列一元二次方程的近似根.
(1)x2-2x-1=0;(2)x2+5=4x.
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(15):6.3 二次函数与一元二次方程(解析版)
题型:解答题
如图,直线y=x+m和抛物线y=x
2+bx+c都经过点A(1,0),B(3,2).
(1)求m的值和抛物线的解析式;
(2)求不等式x
2+bx+c>x+m的解集.(直接写出答案)
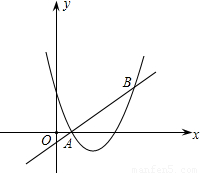
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(16):6.4 二次函数的应用(解析版)
题型:选择题
向上发射一枚炮弹,经x秒后的高度为y公尺,且时间与高度关系为y=ax2+bx.若此炮弹在第7秒与第14秒时的高度相等,则在下列哪一个时间的高度是最高的( )
A.第8秒
B.第10秒
C.第12秒
D.第15秒
查看答案和解析>>
科目:
来源:第6章《二次函数》常考题集(16):6.4 二次函数的应用(解析版)
题型:选择题
一个运动员打尔夫球,若球的飞行高度y(m)与水平距离x(m)之间的函数表达式为y=-
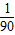
(x-30)
2+10,则高尔夫球在飞行过程中的最大高度为( )
A.10m
B.20m
C.30m
D.60m
查看答案和解析>>

 ,求这个二次函数的解析式.
,求这个二次函数的解析式. ,求m的值,并求出该函数图象的顶点坐标.
,求m的值,并求出该函数图象的顶点坐标.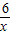 的图象(如图所示),利用图象求方程
的图象(如图所示),利用图象求方程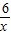 -x+3=0的近似解.(结果保留两个有效数字)
-x+3=0的近似解.(结果保留两个有效数字)


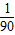 (x-30)2+10,则高尔夫球在飞行过程中的最大高度为( )
(x-30)2+10,则高尔夫球在飞行过程中的最大高度为( )