相关习题
0 127488 127496 127502 127506 127512 127514 127518 127524 127526 127532 127538 127542 127544 127548 127554 127556 127562 127566 127568 127572 127574 127578 127580 127582 127583 127584 127586 127587 127588 127590 127592 127596 127598 127602 127604 127608 127614 127616 127622 127626 127628 127632 127638 127644 127646 127652 127656 127658 127664 127668 127674 127682 366461
科目:
来源:第6章《二次函数》中考题集(43):6.4 二次函数的应用(解析版)
题型:解答题
在平面直角坐标系xOy中,抛物线y=mx
2+2
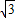
mx+n经过P(
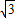
,5),A(0,2)两点.
(1)求此抛物线的解析式;
(2)设抛物线的顶点为B,将直线AB沿y轴向下平移两个单位得到直线l,直线l与抛物线的对称轴交于C点,求直线l的解析式;
(3)在(2)的条件下,求到直线OB,OC,BC距离相等的点的坐标.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(43):6.4 二次函数的应用(解析版)
题型:解答题
已知抛物线y=x
2-2x+a与直线y=x+1有两个公共点A(x
1,y
1),B(x
2,y
2),且x
2>x
1≥0.
(1)求抛物线的对称轴,并在所给坐标系中画出对称轴和直线y=x+1;
(2)试求a的取值范围;
(3)若AE⊥x,E为垂足,BF⊥x轴,F为垂足,试求S
梯形ABFE的最大值.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(45):6.4 二次函数的应用(解析版)
题型:解答题
已知:如图,抛物线y=-

的图象与x轴分别交于A,B两点,与y轴交于C点,⊙M经过原点O及点A、C,点D是劣弧

上一动点(D点与A、O不重合).
(1)求抛物线的顶点E的坐标;
(2)求⊙M的面积;
(3)连CD交AO于点F,延长CD至G,使FG=2,试探究,当点D运动到何处时,直线GA与⊙M相切,并请说明理由.

查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(45):6.4 二次函数的应用(解析版)
题型:解答题
已知P(m,a)是抛物线y=ax
2上的点,且点P在第一象限.
(1)求m的值
(2)直线y=kx+b过点P,交x轴的正半轴于点A,交抛物线于另一点M.
①当b=2a时,∠OPA=90°是否成立?如果成立,请证明;如果不成立,举出一个反例说明;
②当b=4时,记△MOA的面积为S,求

的最大值.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(45):6.4 二次函数的应用(解析版)
题型:解答题
如图1,连接△ABC的各边中点得到一个新的△A
1B
1C
1,又连接△A
1B
1C
1的各边中点得到△A
2B
2C
2,如此无限继续下去,得到一系列三角形:△ABC,△A
1B
1C
1,△A
2B
2C
2,…
已知A(0,0),B(3,0),C(2,2).
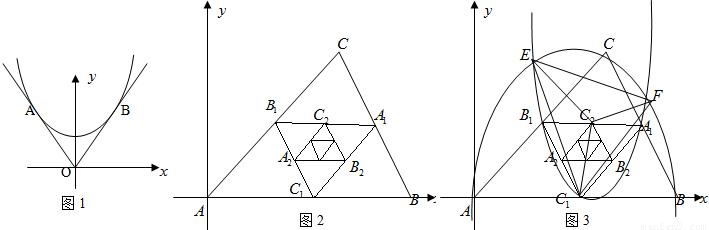
(1)求这一系列三角形趋向于一个点M的坐标;
(2)如图2,分别求出经过A,B,C三点的抛物线解析式和经过A
1,B
1,C
1三点的抛物线解析式;
(3)设两抛物线的交点分别为E、F,连接EF、EC
1、FC
1、EC
2、FC
2、C
1C
2,问:C
2与△EC
1F的关系是什么?
(4)如图3,问:A,A
2,C,C
2四点可不可能在同一条抛物线上,试说明理由.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(45):6.4 二次函数的应用(解析版)
题型:解答题
已知抛物线y=ax
2+b(a>0,b>0),函数y=b|x|
问:(1)如图,当抛物线y=ax
2+b与函数y=b|x|相切于AB两点时,a、b满足的关系;
(2)满足(1)题条件,则三角形AOB的面积为多少?
(3)满足条件(2),则三角形AOB的内心与抛物线的最低点间的距离为多少?
(4)若不等式ax
2+b>b|x|在实数范围内恒成立,则a、b满足什么关系?
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(45):6.4 二次函数的应用(解析版)
题型:解答题
已知抛物线y=

x
2+bx+c经过点(1,-1)和C(0,-1),且与x轴交于A、B两点(A在B左边),直
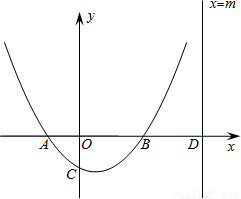
线x=m(m>0)与x轴交于点D.
(1)求抛物线的解析式;
(2)在第一象限内,直线x上是否存在点P,使得以P、B、D为顶点的三角形与△OBC全等?若存在,求出点P坐标;若不存在,说明理由;
(3)在(2)的情况下,过点P作x轴的平行线交抛物线于点Q,四边形AOPQ能否为平行四边形?若能,求Q点坐标;若不能,说明理由.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(45):6.4 二次函数的应用(解析版)
题型:解答题
(人教版)已知:二次函数y=x
2-(m+1)x+m的图象交x轴于A(x
1,0)、B(x
2,0)两点,交y轴正半轴于点C,且x
12+x
22=10.
(1)求此二次函数的解析式;
(2)是否存在过点D(0,-

)的直线与抛物线交于点M、N,与x轴交于点E,使得点M、N关于点E对称?若存在,求直线MN的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(45):6.4 二次函数的应用(解析版)
题型:解答题
在平面直角坐标系中,抛物线交x轴于A,B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,-3).
(1)求这个抛物线的解析式;
(2)在x轴上方平行于x轴的一条直线交抛物线于M,N两点,以MN为直径作圆与x轴相切,求此圆的直径;
(3)在抛物线的对称轴上是否存在一点P,使点P到B,C两点间的距离之差最大?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(45):6.4 二次函数的应用(解析版)
题型:解答题
已知抛物线y=ax2+bx+c(a>0)的顶点是C(0,1),直线l:y=-ax+3与这条抛物线交于P、Q两点,与x轴、y轴分别交于点M和N.
(1)设点P到x轴的距离为2,试求直线l的函数关系式;
(2)若线段MP与PN的长度之比为3:1,试求抛物线的函数关系式.
查看答案和解析>>

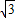 mx+n经过P(
mx+n经过P( ,5),A(0,2)两点.
,5),A(0,2)两点.

 的图象与x轴分别交于A,B两点,与y轴交于C点,⊙M经过原点O及点A、C,点D是劣弧
的图象与x轴分别交于A,B两点,与y轴交于C点,⊙M经过原点O及点A、C,点D是劣弧 上一动点(D点与A、O不重合).
上一动点(D点与A、O不重合).
 的最大值.
的最大值.

 x2+bx+c经过点(1,-1)和C(0,-1),且与x轴交于A、B两点(A在B左边),直
x2+bx+c经过点(1,-1)和C(0,-1),且与x轴交于A、B两点(A在B左边),直 线x=m(m>0)与x轴交于点D.
线x=m(m>0)与x轴交于点D. )的直线与抛物线交于点M、N,与x轴交于点E,使得点M、N关于点E对称?若存在,求直线MN的解析式;若不存在,请说明理由.
)的直线与抛物线交于点M、N,与x轴交于点E,使得点M、N关于点E对称?若存在,求直线MN的解析式;若不存在,请说明理由.