相关习题
0 127512 127520 127526 127530 127536 127538 127542 127548 127550 127556 127562 127566 127568 127572 127578 127580 127586 127590 127592 127596 127598 127602 127604 127606 127607 127608 127610 127611 127612 127614 127616 127620 127622 127626 127628 127632 127638 127640 127646 127650 127652 127656 127662 127668 127670 127676 127680 127682 127688 127692 127698 127706 366461
科目:
来源:第6章《二次函数》中考题集(33):6.4 二次函数的应用(解析版)
题型:解答题
如图,在平面直角坐标系中,将一块腰长为
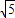
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点B在抛物线y=ax
2+ax-2上
(1)点A的坐标为______,点B的坐标为______;
(2)抛物线的关系式为______;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)将三角板ABC绕顶点A逆时针方向旋转90°,到达△AB′C″的位置.请判断点B′、C″是否在(2)中的抛物线上,并说明理由.

查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(33):6.4 二次函数的应用(解析版)
题型:解答题
(附加题:如果你的全卷得分不足150分,则本题的得分记入总分,但记入总分后全卷得分不得超过150分,超过按150分算.)
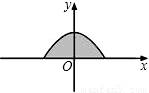
如图是二次函数y=-

x
2+2的图象在x轴上方的一部分,若这段图象与x轴所围成的阴影部分面积为S,试求出S取值的一个范围.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(34):6.4 二次函数的应用(解析版)
题型:解答题
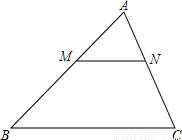
如图,已知一个三角形纸片ABC,BC边的长为8,BC边上的高为6,∠B和∠C都为锐角,M为AB一动点(点M与点A、B不重合),过点M作MN∥BC,交AC于点N,在△AMN中,设MN的长为x,MN上的高为h.
(1)请你用含x的代数式表示h;
(2)将△AMN沿MN折叠,使△AMN落在四边形BCNM所在平面,设点A落在平面的点为A
1,△A
1MN与四边形BCNM重叠部分的面积为y,当x为何值时,y最大,最大值为多少.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(34):6.4 二次函数的应用(解析版)
题型:解答题
矩形OABC在平面直角坐标系中位置如图所示,A、C两点的坐标分别为A(6,0),C(0,-3),直线y=-

x与BC边相交于D点.
(1)求点D的坐标;
(2)若抛物线y=ax
2-

x经过点A,试确定此抛物线的表达式;
(3)设(2)中的抛物线的对称轴与直线OD交于点M,点P为对称轴上一动点,以P、O、M为顶点的三角形与△OCD相似,求符合条件的点P的坐标.

查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(34):6.4 二次函数的应用(解析版)
题型:解答题

如图,已知抛物线y=

x
2+bx+c与坐标轴交于A、B、C三点,A点的坐标为(-1,0),过点C的直线y=
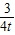
x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
(1)填空:点C的坐标是______,b=______,c=______;
(2)求线段QH的长(用含t的式子表示);
(3)依点P的变化,是否存在t的值,使以P、H、Q为顶点的三角形与△COQ相似?若存在,求出所有t的值;若不存在,说明理由.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(34):6.4 二次函数的应用(解析版)
题型:解答题
如图,已知抛物线y=a(x-1)
2+3
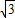
(a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连接BC.
(1)求该抛物线的解析式;
(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为t(s).问当t为何值时,四边形DAOP分别为平行四边形,直角梯形,等腰梯形?
(3)若OC=OB,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t(s),连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.

查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(34):6.4 二次函数的应用(解析版)
题型:解答题
已知,如图1,过点E(0,-1)作平行于x轴的直线l,抛物线y=

x
2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF.
(1)求点A、B、F的坐标;
(2)求证:CF⊥DF;
(3)点P是抛物线y=

x
2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(34):6.4 二次函数的应用(解析版)
题型:解答题
如图所示,已知实数m是方程x
2-8x+16=0的一个实数根,抛物线y=
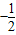
x
2+bx+c交x轴于点A(m,0)和点B,交y轴于点C(0,m).
(1)求这个抛物线的解析式;
(2)设点D为线段AB上的一个动点,过D作DE∥BC交AC于点E,又过D作DF∥AC交BC于点F,当四边形DECF的面积最大时,求点D的坐标;
(3)设△AOC的外接圆为⊙G,若M是⊙G的优弧ACO上的一个动点,连接AM、OM,问在这个抛物线位于y轴左侧的图象上是否存在点N,使得∠NOB=∠AMO?若存在,试求出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(34):6.4 二次函数的应用(解析版)
题型:解答题
如图,已知抛物线C
1:y=a(x+2)
2-5的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1)求P点坐标及a的值;
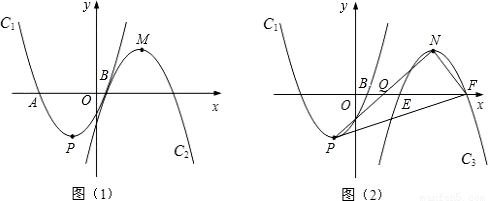
(2)如图(1),抛物线C
2与抛物线C
1关于x轴对称,将抛物线C
2向右平移,平移后的抛物线记为C
3,C
3的顶点为M,当点P、M关于点B成中心对称时,求C
3的解析式;
(3)如图(2),点Q是x轴正半轴上一点,将抛物线C
1绕点Q旋转180°后得到抛物线C
4.抛物线C
4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(34):6.4 二次函数的应用(解析版)
题型:解答题
如图,已知抛物线的顶点为M(5,6),且经过点C(-1,0).
(1)求抛物线的解析式;
(2)设抛物线与y轴交于点A,过A作AB∥x轴,交抛物线于另一点B,则抛物线上存在点P,使△ABP的面积等于△ABO的面积,请求出所有符合条件的点P的坐标;
(3)将抛物线向右平移,使抛物线经过点(5,0),请直接答出曲线段CM(抛物线图象的一部分,如图中的粗线所示)在平移过程中所扫过的面积.

查看答案和解析>>

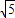 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点B在抛物线y=ax2+ax-2上
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点B在抛物线y=ax2+ax-2上
 x2+2的图象在x轴上方的一部分,若这段图象与x轴所围成的阴影部分面积为S,试求出S取值的一个范围.
x2+2的图象在x轴上方的一部分,若这段图象与x轴所围成的阴影部分面积为S,试求出S取值的一个范围.

 x与BC边相交于D点.
x与BC边相交于D点. x经过点A,试确定此抛物线的表达式;
x经过点A,试确定此抛物线的表达式;
 如图,已知抛物线y=
如图,已知抛物线y= x2+bx+c与坐标轴交于A、B、C三点,A点的坐标为(-1,0),过点C的直线y=
x2+bx+c与坐标轴交于A、B、C三点,A点的坐标为(-1,0),过点C的直线y=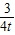 x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.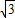 (a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连接BC.
(a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连接BC.
 x2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF.
x2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF. x2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
x2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
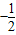 x2+bx+c交x轴于点A(m,0)和点B,交y轴于点C(0,m).
x2+bx+c交x轴于点A(m,0)和点B,交y轴于点C(0,m).

