相关习题
0 127524 127532 127538 127542 127548 127550 127554 127560 127562 127568 127574 127578 127580 127584 127590 127592 127598 127602 127604 127608 127610 127614 127616 127618 127619 127620 127622 127623 127624 127626 127628 127632 127634 127638 127640 127644 127650 127652 127658 127662 127664 127668 127674 127680 127682 127688 127692 127694 127700 127704 127710 127718 366461
科目:
来源:第6章《二次函数》中考题集(29):6.4 二次函数的应用(解析版)
题型:解答题
已知二次函数y=x
2-2x-3的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)求点A、B、C、D的坐标,并在下面直角坐标系中画出该二次函数的大致图象;
(2)说出抛物线y=x
2-2x-3可由抛物线y=x
2如何平移得到?
(3)求四边形OCDB的面积.

查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(29):6.4 二次函数的应用(解析版)
题型:解答题
如图①,抛物线经过点A(12,0)、B(-4,0)、C(0,-12).顶点为M,过点A的直线y=kx-4交y轴于点N.
(1)求该抛物线的函数关系式和对称轴;
(2)试判断△AMN的形状,并说明理由;
(3)将AN所在的直线l向上平移.平移后的直线l与x轴和y轴分别交于点D、E(如图②).当直线l平移时(包括l与直线AN重合),在抛物线对称轴上是否存在点P,使得△PDE是以DE为直角边的等腰直角三角形?若存在,直接写出所有满足条件的点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(29):6.4 二次函数的应用(解析版)
题型:解答题
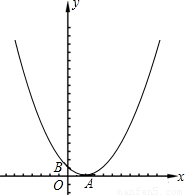
如图所示,已知抛物线
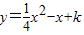
的图象与y轴相交于点B(0,1),点C(m,n)在该抛物线图象上,且以BC为直径的⊙M恰好经过顶点A.
(1)求k的值;
(2)求点C的坐标;
(3)若点P的纵坐标为t,且点P在该抛物线的对称轴l上运动,试探索:
①当S
1<S<S
2时,求t的取值范围(其中:S为△PAB的面积,S
1为△OAB的面积,S
2为四边形OACB的面积);
②当t取何值时,点P在⊙M上.(写出t的值即可)
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(30):6.4 二次函数的应用(解析版)
题型:解答题
如图,在平面直角坐标系xoy中,抛物线y=x
2向左平移1个单位,再向下平移4个单位,得到抛物线y=(x-h)
2+k,所得抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,顶点为D.
(1)求h、k的值;
(2)判断△ACD的形状,并说明理由;
(3)在线段AC上是否存在点M,使△AOM与△ABC相似?若存在,求出点M的坐标;若不存在,说明理由.

查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(30):6.4 二次函数的应用(解析版)
题型:解答题
如图,直线y=x-3于x轴、y轴分别交于B、C;两点,抛物线y=x
2+bx+c同时经过B、C两点,点

A是抛物线与x轴的另一个交点.
(1)求抛物线的函数表达式;
(2)若点P在线段BC上,且S
△PAC=

S
△PAB,求点P的坐标.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(30):6.4 二次函数的应用(解析版)
题型:解答题
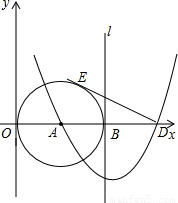
如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求此切线长;
(3)点F是切线DE上的一个动点,当△BFD与EAD△相似时,求出BF的长.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(30):6.4 二次函数的应用(解析版)
题型:解答题
如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x
2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
(1)求线段OA所在直线的函数解析式;
(2)设抛物线顶点M的横坐标为m,
①用m的代数式表示点P的坐标;
②当m为何值时,线段PB最短;
(3)当线段PB最短时,相应的抛物线上是否存在点Q,使△QMA的面积与△PMA的面积相等?若存在,请求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(30):6.4 二次函数的应用(解析版)
题型:解答题
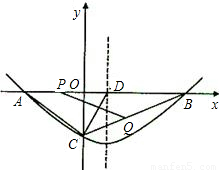
已知抛物线y=ax
2+bx+c(a>0)的图象经过点B(12,0)和C(0,-6),对称轴为x=2.
(1)求该抛物线的解析式;
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点Q以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PQ被直线CD垂直平分?若存在,请求出此时的时间t(秒)和点Q的运动速度;若不存在,请说明理由;
(3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(30):6.4 二次函数的应用(解析版)
题型:解答题
如图,已知点A(-3,0)和B(1,0),直线y=kx-4经过点A并且与y轴交于点C.
(1)求点C的坐标;
(2)求经过A、B、C三点的抛物线的解析式和对称轴;
(3)半径为1个单位长度的动圆⊙P的圆心P始终在抛物线的对称轴上.当点P的纵坐标为5时,将⊙P以每秒1个单位长度的速度在抛物线的对称轴上移动.那么,经过几秒,⊙P与直线AC开始有公共点?经过几秒后,⊙P与直线AC不再有公共点?

查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(30):6.4 二次函数的应用(解析版)
题型:解答题
如图所示,已知直线y=

x与抛物线y=ax
2+b(a≠0)交于A(-4,-2),B(6,3)两点.抛物线与y轴的交点为C.
(1)求这个抛物线的解析式;
(2)在抛物线上存在点M,是△MAB是以AB为底边的等腰三角形,求点M的坐标;
(3)在抛物线上是否存在点P使得△PAC的面积是△ABC面积的

?若存在,试求出此时点P的坐标;若不存在,请说明理由.

查看答案和解析>>



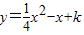 的图象与y轴相交于点B(0,1),点C(m,n)在该抛物线图象上,且以BC为直径的⊙M恰好经过顶点A.
的图象与y轴相交于点B(0,1),点C(m,n)在该抛物线图象上,且以BC为直径的⊙M恰好经过顶点A.

 A是抛物线与x轴的另一个交点.
A是抛物线与x轴的另一个交点. S△PAB,求点P的坐标.
S△PAB,求点P的坐标.



 x与抛物线y=ax2+b(a≠0)交于A(-4,-2),B(6,3)两点.抛物线与y轴的交点为C.
x与抛物线y=ax2+b(a≠0)交于A(-4,-2),B(6,3)两点.抛物线与y轴的交点为C. ?若存在,试求出此时点P的坐标;若不存在,请说明理由.
?若存在,试求出此时点P的坐标;若不存在,请说明理由.