相关习题
0 127547 127555 127561 127565 127571 127573 127577 127583 127585 127591 127597 127601 127603 127607 127613 127615 127621 127625 127627 127631 127633 127637 127639 127641 127642 127643 127645 127646 127647 127649 127651 127655 127657 127661 127663 127667 127673 127675 127681 127685 127687 127691 127697 127703 127705 127711 127715 127717 127723 127727 127733 127741 366461
科目:
来源:第6章《二次函数》中考题集(18):6.3 二次函数与一元二次方程(解析版)
题型:解答题
已知一元二次方程x2+px+q+1=0的一根为2.
(1)求q关于p的关系式;
(2)求证:抛物线y=x2+px+q与x轴有两个交点;
(3)设抛物线y=x2+px+q的顶点为M,且与x轴相交于A(x1,0)、B(x2,0)两点,求使△AMB面积最小时的抛物线的解析式.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(18):6.3 二次函数与一元二次方程(解析版)
题型:解答题
(1)用配方法把二次函数y=x2-4x+3变成y=(x-h)2+k的形成.
(2)在直角坐标系中画出y=x2-4x+3的图象.
(3)若A(x1,y1),B(x2,y2)是函数y=x2-4x+3图象上的两点,且x1<x2<1,请比较y1,y2的大小关系.(直接写结果)
(4)把方程x2-4x+3=2的根在函数y=x2-4x+3的图象上表示出来.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(18):6.3 二次函数与一元二次方程(解析版)
题型:解答题
已知二次函数y=x
2+ax+a-2.
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点;
(2)设a<0,当此函数图象与x轴的两个交点的距离为
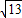
时,求出此二次函数的解析式;
(3)若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为
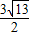
?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(18):6.3 二次函数与一元二次方程(解析版)
题型:解答题
如图,抛物线y=-

x
2+

x+2与x轴交于A、B两点,与y轴交于C点.
(1)求A、B、C三点的坐标;
(2)证明:△ABC为直角三角形;
(3)在抛物线上除C点外,是否还存在另外一个点P,使△ABP是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(18):6.3 二次函数与一元二次方程(解析版)
题型:解答题
如图,已知抛物线y=-

x
2+
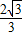
x+
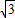
与x轴的两个交点为A、B,与y轴交于点C.
(1)求A,B,C三点的坐标;
(2)求证:△ABC是直角三角形;
(3)若坐标平面内的点M,使得以点M和三点A、B、C为顶点的四边形是平行四边形,求点M的坐标.(直接写出点的坐标,不必写求解过程)

查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(18):6.3 二次函数与一元二次方程(解析版)
题型:解答题
已知关于x的二次函数y=x2-(2m-1)x+m2+3m+4.
(1)探究m满足什么条件时,二次函数y的图象与x轴的交点的个数;
(2)设二次函数y的图象与x轴的交点为A(x1,0),B(x2,0),且x12+x22=5,与y轴的交点为C,它的顶点为M,求直线CM的解析式.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(18):6.3 二次函数与一元二次方程(解析版)
题型:解答题
已知关于x的函数y=ax2+x+1(a为常数)
(1)若函数的图象与x轴恰有一个交点,求a的值;
(2)若函数的图象是抛物线,且顶点始终在x轴上方,求a的取值范围.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(18):6.3 二次函数与一元二次方程(解析版)
题型:解答题
已知抛物线y=3ax2+2bx+c,
(Ⅰ)若a=b=1,c=-1,求该抛物线与x轴公共点的坐标;
(Ⅱ)若a=b=1,且当-1<x<1时,抛物线与x轴有公共点,求c的取值范围;
(Ⅲ)若a+b+c=0,且x1=0时,对应的y1>0;x2=1时,对应的y2>0,试判断当0<x<1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(18):6.3 二次函数与一元二次方程(解析版)
题型:解答题
已知两个关于x的二次函数y1与y2,y1=a(x-k)2+2(k>0),y1+y2=x2+6x+12;当x=k时,y2=17;且二次函数y2的图象的对称轴是直线x=-1.
(1)求k的值;
(2)求函数y1,y2的表达式;
(3)在同一直角坐标系内,问函数y1的图象与y2的图象是否有交点?请说明理由.
查看答案和解析>>
科目:
来源:第6章《二次函数》中考题集(18):6.3 二次函数与一元二次方程(解析版)
题型:解答题
已知:关于x的一元二次方程mx
2-(3m+2)x+2m+2=0(m>0).
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x
1,x
2(其中x
1<x
2).若y是关于m的函数,且y=x
2-2x
1,求这个函数的解析式;
(3)在(2)的条件下,结合函数的图象回答:当自变量m的取值范围满足什么条件时,y≤2m.

查看答案和解析>>

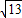 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;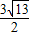 ?若存在,求出P点坐标;若不存在,请说明理由.
?若存在,求出P点坐标;若不存在,请说明理由. x2+
x2+ x+2与x轴交于A、B两点,与y轴交于C点.
x+2与x轴交于A、B两点,与y轴交于C点.
 x2+
x2+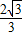 x+
x+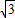 与x轴的两个交点为A、B,与y轴交于点C.
与x轴的两个交点为A、B,与y轴交于点C.
