
科目: 来源:第30章《样本与总体》中考题集(15):30.2 用样本估计总体(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第30章《样本与总体》中考题集(15):30.2 用样本估计总体(解析版) 题型:解答题
| 月用水量(吨) | 3 | 4 | 5 | 7 | 8 | 9 | 10 |
| 户数 | 4 | 3 | 5 | 11 | 4 | 2 | 1 |
查看答案和解析>>
科目: 来源:第30章《样本与总体》中考题集(15):30.2 用样本估计总体(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第30章《样本与总体》中考题集(15):30.2 用样本估计总体(解析版) 题型:解答题
| 株序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 成熟西红柿个数 | 2 | 5 | 2 | 8 | 6 | 2 | 5 | 7 | 9 | 4 |

查看答案和解析>>
科目: 来源:第30章《样本与总体》中考题集(15):30.2 用样本估计总体(解析版) 题型:解答题
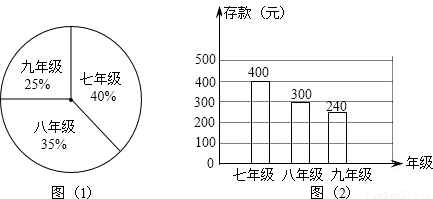
查看答案和解析>>
科目: 来源:第30章《样本与总体》中考题集(15):30.2 用样本估计总体(解析版) 题型:解答题
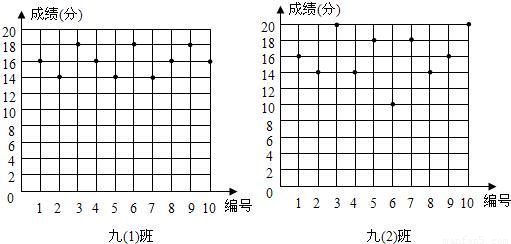
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| 九(1)班 | 16 | 16 | |
| 九(2)班 | 16 |
查看答案和解析>>
科目: 来源:第30章《样本与总体》中考题集(15):30.2 用样本估计总体(解析版) 题型:解答题
| 次 数 | 一 | 二 | 三 | 四 | 五 |
| 分 数 | 46 | 47 | 48 | 49 | 50 |
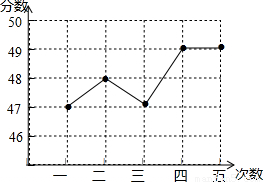
| 中位数 | 平均数 | 方差 | |
| 甲 | 48 | 2 | |
| 乙 | 48 | 48 |
查看答案和解析>>
科目: 来源:第30章《样本与总体》中考题集(16):30.2 用样本估计总体(解析版) 题型:解答题
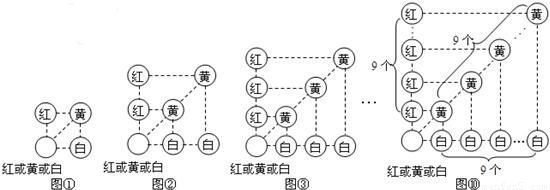
查看答案和解析>>
科目: 来源:第30章《样本与总体》中考题集(16):30.2 用样本估计总体(解析版) 题型:解答题
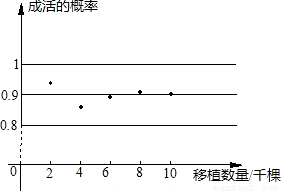
查看答案和解析>>
科目: 来源:第30章《样本与总体》中考题集(16):30.2 用样本估计总体(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com