
科目: 来源:第27章《二次函数》中考题集(50):27.3 实践与探索(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(50):27.3 实践与探索(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(50):27.3 实践与探索(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(50):27.3 实践与探索(解析版) 题型:解答题
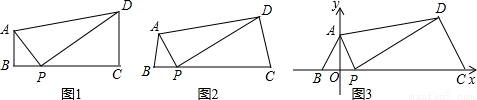
 如图,直线y=-3x-3分别交x轴、y轴于A、B两点,△AOB绕点O按逆时针方向旋转90°后得到△DOC,抛物线y=ax2+bx+c经过A、B、C三点.
如图,直线y=-3x-3分别交x轴、y轴于A、B两点,△AOB绕点O按逆时针方向旋转90°后得到△DOC,抛物线y=ax2+bx+c经过A、B、C三点.查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(50):27.3 实践与探索(解析版) 题型:解答题
 ),且△AOB∽△BOC.
),且△AOB∽△BOC.
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(51):27.3 实践与探索(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(51):27.3 实践与探索(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(51):27.3 实践与探索(解析版) 题型:解答题
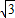 ),∠BCO=60°,OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.
),∠BCO=60°,OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.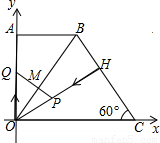
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(51):27.3 实践与探索(解析版) 题型:解答题
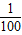 x2+bx(b为常数).在通电情况,高压电线周围12米内为非安全区域.请问3.2米高的车辆从高压电线下方通过时,是否有危险,并说明理由.
x2+bx(b为常数).在通电情况,高压电线周围12米内为非安全区域.请问3.2米高的车辆从高压电线下方通过时,是否有危险,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com