
科目: 来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版) 题型:解答题
查看答案和解析>>
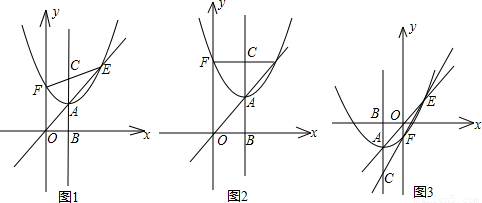
科目: 来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版) 题型:解答题
 ,点E、F、B、C在同一直线上,且FB=1cm,矩形从F点开始以1cm/s的速度沿直线FC向右运动,当边GF所在直线到达D点时即停止.
,点E、F、B、C在同一直线上,且FB=1cm,矩形从F点开始以1cm/s的速度沿直线FC向右运动,当边GF所在直线到达D点时即停止. cm/s的速度运动,矩形停止时点Q也即停止运动,则点Q在矩形一边上运动的时间为多少s?
cm/s的速度运动,矩形停止时点Q也即停止运动,则点Q在矩形一边上运动的时间为多少s?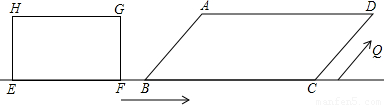
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版) 题型:解答题
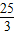 与x轴交于A、B两点(点A在左边),且过点D(5,-3),顶点为M,直线MD交x轴于点F.
与x轴交于A、B两点(点A在左边),且过点D(5,-3),顶点为M,直线MD交x轴于点F.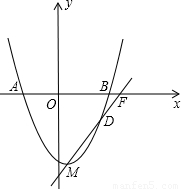
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版) 题型:解答题
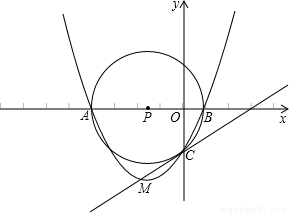
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(40):27.3 实践与探索(解析版) 题型:解答题
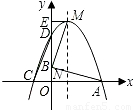
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(40):27.3 实践与探索(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(40):27.3 实践与探索(解析版) 题型:解答题
 x2-
x2-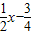 交x轴于A,B两点,顶点为D.以BA为直径作半圆,圆心为M,半圆交y轴负半轴于C.
交x轴于A,B两点,顶点为D.以BA为直径作半圆,圆心为M,半圆交y轴负半轴于C.
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(40):27.3 实践与探索(解析版) 题型:解答题
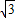 <x2,且抛物线的顶点在直线x=
<x2,且抛物线的顶点在直线x= 的右侧,求a的取值范围.
的右侧,求a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com