相关习题
0 128022 128030 128036 128040 128046 128048 128052 128058 128060 128066 128072 128076 128078 128082 128088 128090 128096 128100 128102 128106 128108 128112 128114 128116 128117 128118 128120 128121 128122 128124 128126 128130 128132 128136 128138 128142 128148 128150 128156 128160 128162 128166 128172 128178 128180 128186 128190 128192 128198 128202 128208 128216 366461
科目:
来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版)
题型:解答题
如图,正方形ABCD的边长为3a,两动点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,对应边EG=BC,B、E、C、G在一直线上.
(1)若BE=a,求DH的长;
(2)当E点在BC边上的什么位置时,△DHE的面积取得最小值?并求该三角形面积的最小值.

查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c的对称轴是经过点(2,0)且与y轴平行的直线,抛物线与x轴相交于点A(1,0),与y轴相交于点B(0,3),其在对称轴左侧的图象如图所示.
(1)求抛物线所对应的函数关系式,并写出抛物线的顶点坐标;
(2)画出抛物线在对称轴右侧的图象,并根据图象,写出当x为何值时,y<0.

查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版)
题型:解答题
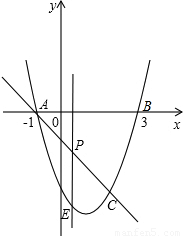
如图,抛物线y=x
2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版)
题型:解答题
已知抛物线y=kx2-2kx+9-k(k为常数,k≠0),且当x>0时,y>1.
(1)求抛物线的顶点坐标;
(2)求k的取值范围;
(3)过动点P(0,n)作直线l⊥y轴,点O为坐标原点.
①当直线l与抛物线只有一个公共点时,求n关于k的函数关系式;
②当直线l与抛物线相交于A、B两点时,是否存在实数n,使得不论k在其取值范围内取任意值时,△AOB的面积为定值?如果存在,求出n的值;如果不存在,说明理由.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版)
题型:解答题
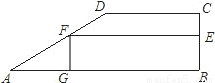
如图,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2a,CD=a,BC=2,四边形BEFG是矩形,点E、F分别在腰BC、AD上,点G在AB上.设FG=x,矩形BEFG的面积为y.
(1)求y关于x的函数关系式;
(2)当矩形BEFG的面积等于梯形ABCD的面积的一半时,求x的值;
(3)当∠DAB=30°时,矩形BEFG是否能成为正方形?若能,求其边长;若不能,请说明理由.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版)
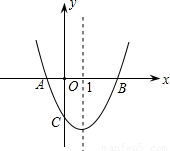
题型:解答题
抛物线y=ax
2+bx+c交x轴于A,B两点,交y轴于点C,对称轴为直线x=1,已知:A(-1,0),C(0,-3).
(1)求抛物线y=ax
2+bx+c的解析式;
(2)求△AOC和△BOC的面积的比;
(3)在对称轴是否存在一个点P,使△PAC的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版)
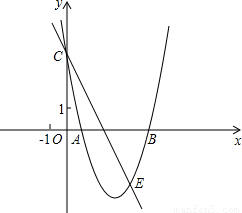
题型:解答题
已知:如图,抛物线y=ax
2+bx+c经过A(1,0)、B(5,0)、C(0,5)三点.
(1)求抛物线的函数关系式;
(2)若过点C的直线y=kx+b与抛物线相交于点E(4,m),请求出△CBE的面积S的值;
(3)在抛物线上求一点P
,使得△ABP
为等腰三角形,并写出P
点的坐标;
附加:(4)除(3)中所求的P
点外,在抛物线上是否还存在其它的点P使得△ABP为等腰三角形?若存在,请求出一共有几个满足条件的点P(要求简要说明理由,但不证明);若不存在这样的点P,请说明理由.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版)
题型:解答题
已知:直线y=x+6交x、y轴于A、C两点,经过A、O两点的抛物线y=ax
2+bx(a<0)的顶点在直线AC上.
(1)求A、C两点的坐标;
(2)求出抛物线的函数关系式;
(3)以B点为圆心,以AB为半径作⊙B,将⊙B沿x轴翻折得到⊙D,试判断直线AC与⊙D的位置关系,并求出BD的长;
(4)若E为⊙B劣弧OC上一动点,连接AE、OE,问在抛物线上是否存在一点M,使∠MOA:∠AEO=2:3?若存在,试求出点M的坐标;若不存在,试说明理由.
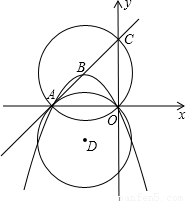
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版)
题型:解答题

如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴y上.
(1)求m的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E,设线段PE的长为h,点P的横坐标为x,求h与x之间的函数关系式,并写出自变量x的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版)
题型:解答题
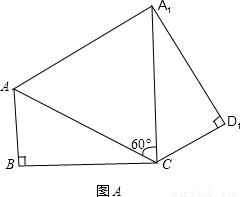
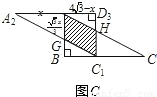
如图,矩形纸片ABCD中,AB=4,BC=4

,将矩形沿对角线AC剪开,解答以下问题:
(1)在△ACD绕点C顺时针旋转60°,△A
1CD
1是旋转后的新位置(图A),求此AA
1的距离;
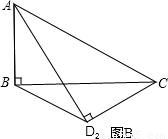
(2)将△ACD沿对角线AC向下翻折(点A、点C位置不动,△ACD和△ABC落在同一平面内),△ACD
2是翻折后的新位置(图B),求此时BD
2的距离;
(3)将△ACD沿CB向左平移,设平移的距离为x(0≤x≤4
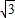
),△A
2C
1D
3是平移后的新位置(图C),若△ABC与△A
2C
1D
3重叠部分的面积为y,求y关于x的函数关系式.

查看答案和解析>>



 如图,抛物线y=x2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
如图,抛物线y=x2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.



 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴y上.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴y上. ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: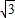 ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.


