
科目: 来源:第27章《二次函数》中考题集(37):27.3 实践与探索(解析版) 题型:解答题
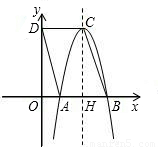 如图,平行四边形ABCD中,AB=4,点D的坐标是(0,8),以点C为顶点的抛物线y=ax2+bx+c经过x轴上的点A,B.
如图,平行四边形ABCD中,AB=4,点D的坐标是(0,8),以点C为顶点的抛物线y=ax2+bx+c经过x轴上的点A,B.查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(37):27.3 实践与探索(解析版) 题型:解答题
 )(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.
)(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.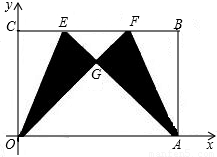
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(37):27.3 实践与探索(解析版) 题型:解答题
 ),现将纸片按如图折叠,AD,DE为折痕,∠OAD=30度.折叠后,点O落在点O1,点C落在线段AB点C1处,并且DO1与DC1在同一直线上.
),现将纸片按如图折叠,AD,DE为折痕,∠OAD=30度.折叠后,点O落在点O1,点C落在线段AB点C1处,并且DO1与DC1在同一直线上.
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(37):27.3 实践与探索(解析版) 题型:解答题
 ,
, ),且与抛物线y2=ax2-ax-1相交于A,B两点.
),且与抛物线y2=ax2-ax-1相交于A,B两点.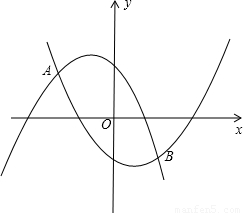
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(37):27.3 实践与探索(解析版) 题型:解答题
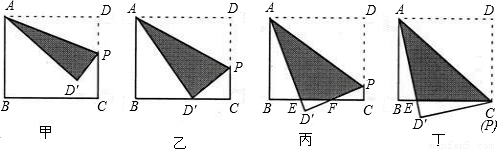
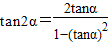 (α≠45°).根据上述阅读材料,求出用x表示y的解析式,并指出x的取值范围.
(α≠45°).根据上述阅读材料,求出用x表示y的解析式,并指出x的取值范围.查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(37):27.3 实践与探索(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(37):27.3 实践与探索(解析版) 题型:解答题
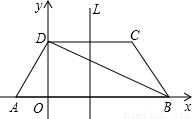
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(37):27.3 实践与探索(解析版) 题型:解答题
 x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(- ,0).
,0).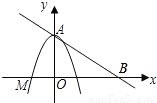
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(37):27.3 实践与探索(解析版) 题型:解答题
 x2+bx+c经过A(0,-4)、B(x1,0)、C(x2,0)三点,且x2-x1=5.
x2+bx+c经过A(0,-4)、B(x1,0)、C(x2,0)三点,且x2-x1=5.
查看答案和解析>>
科目: 来源:第27章《二次函数》中考题集(37):27.3 实践与探索(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com