练习册

  • 练习册
  • 试题
    相关习题
     0  128060  128068  128074  128078  128084  128086  128090  128096  128098  128104  128110  128114  128116  128120  128126  128128  128134  128138  128140  128144  128146  128150  128152  128154  128155  128156  128158  128159  128160  128162  128164  128168  128170  128174  128176  128180  128186  128188  128194  128198  128200  128204  128210  128216  128218  128224  128228  128230  128236  128240  128246  128254  366461 

    科目： 来源：第27章《二次函数》中考题集（23）：27.3 实践与探索（解析版） 题型：解答题

    四川汶川大地震发生后，我市某工厂A车间接到生产一批帐篷的订单，要求必须在12天（含12天）内完成．已知每顶帐篷的成本价为800元，该车间平时每天能生产帐篷20顶．为了加快进度，车间采取工人分批日夜加班，机器满负荷运转的生产方式，生产效率得到了提高．这样，第一天生产了22顶，以后每天生产的帐篷都比前一天多2顶．由于机器损耗等原因，当每天生产的帐篷达到30顶后，每增加1顶帐篷，当天生产的所有帐篷，平均每顶的成本就增加20元．设生产这批帐篷的时间为x天，每天生产的帐篷为y顶．
    （1）直接写出y与x之间的函数关系式，并写出自变量x的取值范围．
    （2）若这批帐篷的订购价格为每顶1200元，该车间决定把获得最高利润的那一天的全部利润捐献给灾区．设该车间每天的利润为W元，试求出W与x之间的函数关系式，并求出该项车间捐献给灾区多少钱？

    查看答案和解析>>

    科目： 来源：第27章《二次函数》中考题集（23）：27.3 实践与探索（解析版） 题型：解答题

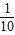    研究所对某种新型产品的产销情况进行了研究，为投资商在甲、乙两地生产并销售该产品提供了如下成果：第一年的年产量为x（吨）时，所需的全部费用y（万元）与x满足关系式y=x2+5x+90，投入市场后当年能全部售出，且在甲、乙两地每吨的售价p甲，p乙（万元）均与x满足一次函数关系．（注：年利润=年销售额-全部费用）
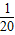    （1）成果表明，在甲地生产并销售x吨时，P甲=-x+14，请你用含x的代数式表示甲地当年的年销售额，并求年利润W甲（万元）与x之间的函数关系式；
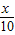    （2）成果表明，在乙地生产并销售x吨时，P乙=-+n（n为常数），且在乙地当年的最大年利润为35万元．试确定n的值；
    （3）受资金、生产能力等多种因素的影响，某投资商计划第一年生产并销售该产品18吨，根据（1），（2）中的结果，请你通过计算帮他决策，选择在甲地还是乙地产销才能获得较大的年利润？
    参考公式：抛物线y=ax2+bx+c（a≠0）的顶点坐标是．

    查看答案和解析>>

    科目： 来源：第27章《二次函数》中考题集（23）：27.3 实践与探索（解析版） 题型：解答题

    小李想用篱笆围成一个周长为60米的矩形场地，矩形面积S（单位：平方米）随矩形一边长x（单位：米）的变化而变化．
    （1）求S与x之间的函数关系式，并写出自变量x的取值范围；
    （2）当x是多少时，矩形场地面积S最大，最大面积是多少？

    查看答案和解析>>

    科目： 来源：第27章《二次函数》中考题集（23）：27.3 实践与探索（解析版） 题型：解答题

    桂林红桥位于桃花江上，是桂林两江四湖的一道亮丽的风景线，该桥的部分横截面如图所示，上方可看作是一个经过A、C、B三点的抛物线，以桥面的水平线为x轴，经过抛物线的顶点C与x轴垂直的直线为y轴，建立直角坐标系，已知此桥垂直于桥面的相邻两柱之间距离为2米（图中用线段AD、CO、BE等表示桥柱）CO=1米，FG=2米．
    （1）求经过A、B、C三点的抛物线的解析式．
    （2）求柱子AD的高度．

    查看答案和解析>>

    科目： 来源：第27章《二次函数》中考题集（23）：27.3 实践与探索（解析版） 题型：解答题

    某宾馆客房部有60个房间供游客居住，当每个房间的定价为每天200元时，房间可以住满．当每个房间每天的定价每增加10元时，就会有一个房间空闲．对有游客入住的房间，宾馆需对每个房间每天支出20元的各种费用．
    设每个房间每天的定价增加x元．求：
    （1）房间每天的入住量y（间）关于x（元）的函数关系式；
    （2）该宾馆每天的房间收费z（元）关于x（元）的函数关系式；
    （3）该宾馆客房部每天的利润w（元）关于x（元）的函数关系式；当每个房间的定价为每天多少元时，w有最大值？最大值是多少？

    查看答案和解析>>

    科目： 来源：第27章《二次函数》中考题集（23）：27.3 实践与探索（解析版） 题型：解答题

    如图，某隧道横截面的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成，最大高度为6米，底部宽度为12米．现以O点为原点，OM所在直线为x轴建立直角坐标系．
    （1）直接写出点M及抛物线顶点P的坐标；
    （2）求出这条抛物线的函数解析式；
    （3）若要搭建一个矩形“支撑架”AD+DC+CB，使C、D点在抛物线上，A、B点在地面OM上，这个“支撑架”总长的最大值是多少？

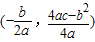    查看答案和解析>>

    科目： 来源：第27章《二次函数》中考题集（23）：27.3 实践与探索（解析版） 题型：解答题

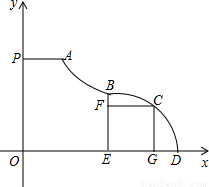    “假日旅乐园”中一种新型水上滑梯如图，其中线段PA表示距离水面（x轴）高度为5m的平台（点P在y轴上）．滑道AB可以看作反比例函数图象的一部分，滑道BCD可以看作是二次函数图象的一部分，两滑道的连接点B为抛物线BCD的顶点，且点B到水面的距离BE=2m，点B到y轴的距离是5m．当小明从上而下滑到点C时，与水面的距离CG=m，与点B的水平距离CF=2m．
    （1）求反比例函数的解析式及其自变量的取值范围．
    （2）求二次函数的解析式及其自变量的取值范围．
    （3）小明从点B滑水面上点D处时，试求他所滑过的水平距离d．

    查看答案和解析>>

    科目： 来源：第27章《二次函数》中考题集（24）：27.3 实践与探索（解析版） 题型：解答题

    为了落实国务院副总理李克强同志到恩施考察时的指示精神，最近，州委州政府又出台了一系列“三农”优惠政策，使农民收入大幅度增加．某农户生产经销一种农副产品，已知这种产品的成本价为20元/千克．市场调查发现，该产品每天的销售量w（千克）与销售价x（元/千克）有如下关系：w=-2x+80．设这种产品每天的销售利润为y（元）．
    （1）求y与x之间的函数关系式；
    （2）当销售价定为多少元时，每天的销售利润最大？最大利润是多少？
    （3）如果物价部门规定这种产品的销售价不得高于28元/千克，该农户想要每天获得150元的销售利润，销售价应定为多少元？

    查看答案和解析>>

    科目： 来源：第27章《二次函数》中考题集（24）：27.3 实践与探索（解析版） 题型：解答题

    如图，河上有一座抛物线桥洞，已知桥下的水面离桥拱顶部3m时，水面宽AB为6m，当水位上升0.5m时：
    （1）求水面的宽度CD为多少米？
    （2）有一艘游船，它的左右两边缘最宽处有一个长方体形状的遮阳棚，此船正对着桥洞在上述河流中航行．
    ①若游船宽（指船的最大宽度）为2m，从水面到棚顶的高度为1.8m，问这艘游船能否从桥洞下通过？
    ②若从水面到棚顶的高度为m的游船刚好能从桥洞下通过，则这艘游船的最大宽度是多少米？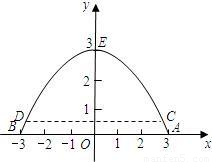

    查看答案和解析>>

    科目： 来源：第27章《二次函数》中考题集（24）：27.3 实践与探索（解析版） 题型：解答题

    如图，足球场上守门员在O处开出一高球，球从离地面1米的A处飞出（A在y轴上），运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M，距地面约4米高，球落地后又一次弹起．据实验测算，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．
    （1）求足球开始飞出到第一次落地时，该抛物线的表达式．
    （2）足球第一次落地点C距守门员多少米？（取4=7）
    （3）运动员乙要抢到第二个落点D，他应再向前跑多少米？（取=5）

    查看答案和解析>>

    同步练习册答案