相关习题
0 128071 128079 128085 128089 128095 128097 128101 128107 128109 128115 128121 128125 128127 128131 128137 128139 128145 128149 128151 128155 128157 128161 128163 128165 128166 128167 128169 128170 128171 128173 128175 128179 128181 128185 128187 128191 128197 128199 128205 128209 128211 128215 128221 128227 128229 128235 128239 128241 128247 128251 128257 128265 366461
科目:
来源:第27章《二次函数》中考题集(20):27.3 实践与探索(解析版)
题型:解答题
已知点A(1,1)在二次函数y=x2-2ax+b图象上.
(1)用含a的代数式表示b;
(2)如果该二次函数的图象与x轴只有一个交点,求这个二次函数的图象的顶点坐标.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(20):27.3 实践与探索(解析版)
题型:解答题
已知:二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,其中点A的坐标是(-2,0),点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OC<OB)是方程x2-10x+24=0的两个根.
(1)求B、C两点的坐标;
(2)求这个二次函数的解析式.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(20):27.3 实践与探索(解析版)
题型:解答题
已知二次函数y=-x
2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
(1)求出b,c的值,并写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.
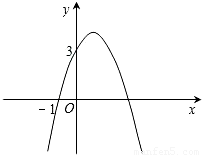
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(20):27.3 实践与探索(解析版)
题型:解答题
已知一元二次方程x2+px+q+1=0的一根为2.
(1)求q关于p的关系式;
(2)求证:抛物线y=x2+px+q与x轴有两个交点;
(3)设抛物线y=x2+px+q的顶点为M,且与x轴相交于A(x1,0)、B(x2,0)两点,求使△AMB面积最小时的抛物线的解析式.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(20):27.3 实践与探索(解析版)
题型:解答题
(1)用配方法把二次函数y=x2-4x+3变成y=(x-h)2+k的形成.
(2)在直角坐标系中画出y=x2-4x+3的图象.
(3)若A(x1,y1),B(x2,y2)是函数y=x2-4x+3图象上的两点,且x1<x2<1,请比较y1,y2的大小关系.(直接写结果)
(4)把方程x2-4x+3=2的根在函数y=x2-4x+3的图象上表示出来.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(20):27.3 实践与探索(解析版)
题型:解答题
已知二次函数y=x
2+ax+a-2.
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点;
(2)设a<0,当此函数图象与x轴的两个交点的距离为

时,求出此二次函数的解析式;
(3)若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为
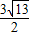
?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(20):27.3 实践与探索(解析版)
题型:解答题
如图,抛物线y=-

x
2+

x+2与x轴交于A、B两点,与y轴交于C点.
(1)求A、B、C三点的坐标;
(2)证明:△ABC为直角三角形;
(3)在抛物线上除C点外,是否还存在另外一个点P,使△ABP是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
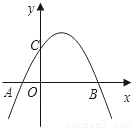
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(20):27.3 实践与探索(解析版)
题型:解答题
如图,已知抛物线y=-
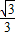
x
2+
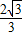
x+

与x轴的两个交点为A、B,与y轴交于点C.
(1)求A,B,C三点的坐标;
(2)求证:△ABC是直角三角形;
(3)若坐标平面内的点M,使得以点M和三点A、B、C为顶点的四边形是平行四边形,求点M的坐标.(直接写出点的坐标,不必写求解过程)

查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(20):27.3 实践与探索(解析版)
题型:解答题
已知关于x的二次函数y=x2-(2m-1)x+m2+3m+4.
(1)探究m满足什么条件时,二次函数y的图象与x轴的交点的个数;
(2)设二次函数y的图象与x轴的交点为A(x1,0),B(x2,0),且x12+x22=5,与y轴的交点为C,它的顶点为M,求直线CM的解析式.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(20):27.3 实践与探索(解析版)
题型:解答题
已知关于x的函数y=ax2+x+1(a为常数)
(1)若函数的图象与x轴恰有一个交点,求a的值;
(2)若函数的图象是抛物线,且顶点始终在x轴上方,求a的取值范围.
查看答案和解析>>


 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;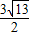 ?若存在,求出P点坐标;若不存在,请说明理由.
?若存在,求出P点坐标;若不存在,请说明理由. x2+
x2+ x+2与x轴交于A、B两点,与y轴交于C点.
x+2与x轴交于A、B两点,与y轴交于C点.
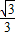 x2+
x2+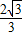 x+
x+ 与x轴的两个交点为A、B,与y轴交于点C.
与x轴的两个交点为A、B,与y轴交于点C.