科目： 来源：第27章《二次函数》中考题集（17）：27.3 实践与探索（解析版） 题型：选择题

科目： 来源：第27章《二次函数》中考题集（17）：27.3 实践与探索（解析版） 题型：选择题

科目： 来源：第27章《二次函数》中考题集（17）：27.3 实践与探索（解析版） 题型：选择题

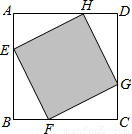
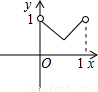
如图，已知：正方形ABCD边长为1，E、F、G、H分别为各边上的点，且AE=BF=CG=DH，设小正方形EFGH的面积为s，AE为x，则s关于x的函数图象大致是（ ）

A．
B．
C．
D．

科目： 来源：第27章《二次函数》中考题集（17）：27.3 实践与探索（解析版） 题型：选择题

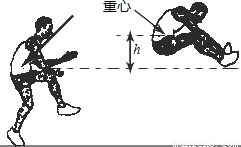
小敏在今年的校运动会跳远比赛中跳出了满意一跳，函数h=3.5t-4.9t²（t的单位：s，h的单位：m）可以描述他跳跃时重心高度的变化，则他起跳后到重心最高时所用的时间是（ ）

A．0.71s
B．0.70s
C．0.63s
D．0.36s

科目： 来源：第27章《二次函数》中考题集（17）：27.3 实践与探索（解析版） 题型：选择题

如图，两条抛物线y₁=-x²+1，y₂=与分别经过点（-2，0），（2，0）且平行于y轴的两条平行线围成的阴影部分的面积为（ ）

A．8
B．6
C．10
D．4

科目： 来源：第27章《二次函数》中考题集（17）：27.3 实践与探索（解析版） 题型：选择题

如图，点A，B的坐标分别为（1，4）和（4，4），抛物线y=a（x-m）²+n的顶点在线段AB上运动（抛物线随顶点一起平移），与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为-3，则点D的横坐标最大值为（ ）

A．-3
B．1
C．5
D．8

科目： 来源：第27章《二次函数》中考题集（17）：27.3 实践与探索（解析版） 题型：选择题

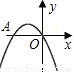
如图，二次函数y=-x²-2x的图象与x轴交于点A、O，在抛物线上有一点P，满足S_△AOP=3，则点P的坐标是（ ）

A．（-3，-3）
B．（1，-3）
C．（-3，-3）或（-3，1）
D．（-3，-3）或（1，-3）

科目： 来源：第27章《二次函数》中考题集（17）：27.3 实践与探索（解析版） 题型：选择题

已知图中的每个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点，请你在图中任意画一条抛物线，问所画的抛物线最多能经过81个格点中的多少个（ ）
A．6
B．7
C．8
D．9

科目： 来源：第27章《二次函数》中考题集（18）：27.3 实践与探索（解析版） 题型：选择题

如图所示是二次函数y=-x²+2的图象在x轴上方的一部分，对于这段图象与x轴所围成的阴影部分的面积，你认为可能的值是（ ）

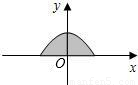
A．4
B．
C．2π
D．8

科目： 来源：第27章《二次函数》中考题集（18）：27.3 实践与探索（解析版） 题型：选择题

如图，记抛物线y=-x²+1的图象与x正半轴的交点为A，将线段OA分成n等份，设分点分别为P₁，P₂，…P_n-1，过每个分点作x轴的垂线，分别与抛物线交于点Q₁，Q₂，…，Q_n-1，再记直角三角形OP₁Q₁，P₁P₂Q₂，…，P_n-2P_n-1Q_n-1的面积分别为S₁，S₂，…，这样就有S₁=，S₂=，…；记W=S₁+S₂+…+S_n-1，当n越来越大时，你猜想W最接近的常数是（ ）

A．
B．
C．
D．