相关习题
0 128112 128120 128126 128130 128136 128138 128142 128148 128150 128156 128162 128166 128168 128172 128178 128180 128186 128190 128192 128196 128198 128202 128204 128206 128207 128208 128210 128211 128212 128214 128216 128220 128222 128226 128228 128232 128238 128240 128246 128250 128252 128256 128262 128268 128270 128276 128280 128282 128288 128292 128298 128306 366461
科目:
来源:第27章《二次函数》中考题集(01):27.1 二次函数(解析版)
题型:选择题
下列函数关系中,是二次函数的是( )
A.在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
B.当距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长C与边长a之间的关系
D.圆心角为120°的扇形面积S与半径R之间的关系
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(01):27.1 二次函数(解析版)
题型:选择题
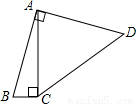
如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
A.y=

B.y=
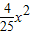
C.y=
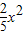
D.y=
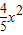
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(01):27.1 二次函数(解析版)
题型:选择题
图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( )

A.y=-2x
2B.y=2x
2C.y=-

x
2D.y=

x
2
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(01):27.1 二次函数(解析版)
题型:选择题
进入夏季后,某电器商场为减少库存,对电热取暖器连续进行两次降价.若设平均每次降价的百分率是x,降价后的价格为y元,原价为a元,则y与x之间的函数关系式为( )
A.y=2a(x-1)
B.y=2a(1-x)
C.y=a(1-x2)
D.y=a(1-x)2
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(01):27.1 二次函数(解析版)
题型:选择题
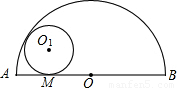
如图,半圆O的直径AB=4,与半圆O内切的动圆O
1与AB切于点M,设⊙O
1的半径为y,AM=x,则y关于x的函数关系式是( )
A.y=-

x
2+
B.y=-x
2+
C.y=-

x
2-
D.y=

x
2-
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(01):27.1 二次函数(解析版)
题型:解答题
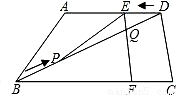
如图,在梯形ABCD中,AD∥BC,AD=6cm,CD=4cm,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题:
(1)当t为何值时,PE∥AB;
(2)设△PEQ的面积为y(cm
2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S
△PEQ=

S
△BCD?若存在,求出此时t的值;若不存在,说明理由;
(4)连接PF,在上述运动过程中,五边形PFCDE的面积是否发生变化?说明理由.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(01):27.1 二次函数(解析版)
题型:解答题

如图,在菱形ABCD中,∠A=60°,AB=4,E是边AB上一动点,过点E作EF⊥AB交AD的延长线于点F,交BD于点M.
(1)请判断△DMF的形状,并说明理由.
(2)设EB=x,△DMF的面积为y,求y与x之间的函数关系式.并写出x的取值范围.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(01):27.1 二次函数(解析版)
题型:解答题
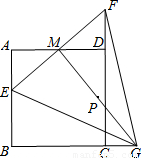
如图,正方形ABCD的边长是2,M是AD的中点,点E从点A出发,沿AB运动到点B停止,连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连接EG、FG.
(1)设AE=x时,△EGF的面积为y,求y关于x的函数关系式,并写出自变量x的取值范围;
(2)P是MG的中点,请直接写出点P的运动路线的长.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(01):27.1 二次函数(解析版)
题型:解答题
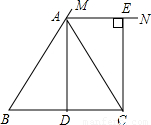
如图,△ABC中AB=AC,BC=6,点D位BC中点,连接AD,AD=4,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)试判断四边形ADCE的形状并说明理由.
(2)将四边形ADCE沿CB以每秒1个单位长度的速度向左平移,设移动时间为t(0≤t≤6)秒,平移后的四边形A’D’C’E’与△ABC重叠部分的面积为S,求S关于t的函数表达式,并写出相应的t的取值范围.
查看答案和解析>>
科目:
来源:第27章《二次函数》中考题集(01):27.1 二次函数(解析版)
题型:解答题
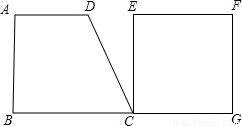
如图,直角梯形ABCD和正方形EFGC的边BC、CG在同一条直线上,AD∥BC,AB⊥BC于点B,AD=4,AB=6,BC=8,直角梯形ABCD的面积与正方形EFGC的面积相等,将直角梯形ABCD沿BG向右平行移动,当点C与点G重合时停止移动.设梯形与正方形重叠部分的面积为S.
(1)求正方形的边长;
(2)设直角梯形ABCD的顶点C向右移动的距离为x,求S与x的函数关系式;
(3)当直角梯形ABCD向右移动时,它与正方形EFGC的重叠部分面积S能否等于直角梯形ABCD面积的一半?若能,请求出此时运动的距离x的值;若不能,请说明理由.
查看答案和解析>>



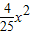
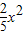
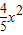

 x2
x2 x2
x2
 x2+
x2+ x2-
x2- x2-
x2- S△BCD?若存在,求出此时t的值;若不存在,说明理由;
S△BCD?若存在,求出此时t的值;若不存在,说明理由;
 如图,在菱形ABCD中,∠A=60°,AB=4,E是边AB上一动点,过点E作EF⊥AB交AD的延长线于点F,交BD于点M.
如图,在菱形ABCD中,∠A=60°,AB=4,E是边AB上一动点,过点E作EF⊥AB交AD的延长线于点F,交BD于点M.

