相关习题
0 128159 128167 128173 128177 128183 128185 128189 128195 128197 128203 128209 128213 128215 128219 128225 128227 128233 128237 128239 128243 128245 128249 128251 128253 128254 128255 128257 128258 128259 128261 128263 128267 128269 128273 128275 128279 128285 128287 128293 128297 128299 128303 128309 128315 128317 128323 128327 128329 128335 128339 128345 128353 366461
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(38):3.3 圆与圆的位置关系(解析版)
题型:解答题
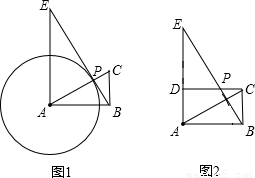
如图1,已知Rt△ABC中,∠CAB=30°,BC=5.过点A作AE⊥AB,且AE=15,连接BE交AC于点P.
(1)求PA的长;
(2)以点A为圆心,AP为半径作⊙A,试判断BE与⊙A是否相切,并说明理由;
(3)如图2,过点C作CD⊥AE,垂足为D.以点A为圆心,r为半径作⊙A;以点C为圆心,R为半径作⊙C.若r和R的大小是可变化的,并且在变化过程中保持⊙A和⊙C相切,且使D点在⊙A的内部,B点在⊙A的外部,求r和R的变化范围.
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(38):3.3 圆与圆的位置关系(解析版)
题型:解答题
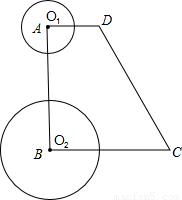
如图,直角梯形ABCD中,AD∥BC,∠A=90°,∠C=60°,AD=3cm,BC=9cm.⊙O
1的圆心O
1从点A开始沿折线A-D-C以1cm/s的速度向点C运动,⊙O
2的圆心O
2从点B开始沿BA边以
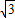
cm/s的速度向点A运动,⊙O
1半径为2cm,⊙O
2的半径为4cm,若O
1、O
2分别从点A、点B同时出发,运动的时间为t.
(1)请求出⊙O
2与腰CD相切时t的值;
(2)在0s<t≤3s范围内,当t为何值时,⊙O
1与⊙O
2外切?
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(38):3.3 圆与圆的位置关系(解析版)
题型:解答题
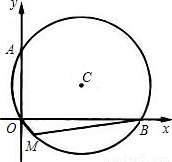
如图,⊙C经过坐标原点O,分别交x轴正半轴、y轴正半轴于点B、A,点B的坐标为(4
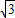
,0),点M在⊙C上,并且∠BMO=120度.
(1)求直线AB的解析式;
(2)若点P是⊙C上的点,过点P作⊙C的切线PN,若∠NPB=30°,求点P的坐标;
(3)若点D是⊙C上任意一点,以B为圆心,BD为半径作⊙B,并且BD的长为正整数.
①问这样的圆有几个?它们与⊙C有怎样的位置关系?
②在这些圆中,是否存在与⊙C所交的弧(指⊙B上的一条弧)为90°的弧,若存在,请给出证明;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(38):3.3 圆与圆的位置关系(解析版)
题型:解答题
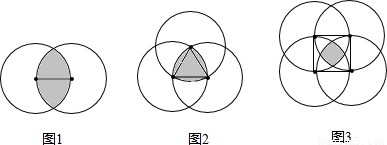
宏远广告公司要为某企业的一种产品设计商标图案,给出了如下几种初步方案,供继续设计选用(设图中圆的半径均为r)
(1)如图1,分别以线段O
1O
2的两个端点为圆心,以这条线段的长为半径作出两个互相交错的圆的图案,试求两圆相交部分的面积;
(2)如图2,分别以等边△O
1O
2O
3的三个顶点为圆心,以其边长为半径,作出三个两两相交的相同的圆,这时,这三个圆相交部分的面积又是多少呢?
(3)如图3,分别以正方形O
1O
2O
3O
4的四个顶点为圆心,以其边长为半径,作出四个相同的圆,这时,这四个圆相交部分的面积又是多少呢?
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(38):3.3 圆与圆的位置关系(解析版)
题型:解答题
如图1,圆O
1与圆O
2都经过A、B两点,经过点A的直线CD与圆O
1交于点C,与圆O
2交于点D.经过点B的直线EF与圆O
1交于点E,与圆O
2交于点F.

(1)求证:CE∥DF;
(2)在图1中,若CD和EF可以分别绕点A和点B转动,当点C与点E重合时(如图2),过点E作直线MN∥DF,试判断直线MN与圆O
1的位置关系,并证明你的结论.
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(38):3.3 圆与圆的位置关系(解析版)
题型:解答题
(1)计算:如图①,直径为a的三等圆⊙O
1、⊙O
2、⊙O
3两两外切,切点分别为A、B、C,求O
1A的长(用含a的代数式表示);
(2)探索:若干个直径为a的圆圈分别按如图②所示的方案一和如图③所示的方案二的方式排放,探索并求出这两种方案中n层圆圈的高度h
n和h
n′(用含n、a的代数式表示);
(3)应用:现有长方体集装箱,其内空长为5米,宽为3.1米,高为3.1米.用这样的集装箱装运长为5米,底面直径(横截面的外圆直径)为0.1米的圆柱形钢管,你认为采用(2)中的哪种方案在该集装箱中装运钢管数最多?并求出一个这样的集装箱最多能装运多少根钢管?(
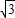
≈1.73)

查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(38):3.3 圆与圆的位置关系(解析版)
题型:解答题
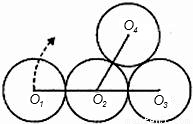
如图,⊙O
1、⊙O
2、⊙O
3、⊙O
4的半径都为1,其中⊙O
1和⊙O
2外切,⊙O
2、⊙O
3,⊙O
4两两外切,并且O
1、O
2、O
3、三点在同一直线上.
(1)请直接写出O
2O
4的长;
(2)若⊙O
1沿图中箭头所示的方向在⊙O
2的圆周上滚动,最后⊙O
1滚动到⊙O
4的位置上,试求在上述滚动过程中圆心O
1移动的距离.(精确到0.01)
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(38):3.3 圆与圆的位置关系(解析版)
题型:解答题
如图,是一盒刚打开的“兰州”牌香烟,图(1)是它的横截面(矩形ABCD),已知每支香烟底面圆的直径是8mm.
(1)矩形ABCD的长AB=______mm;
(2)利用图(2)求矩形ABCD的宽AD.(
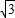
≈1.73,结果精确到0.1mm)


查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(38):3.3 圆与圆的位置关系(解析版)
题型:解答题
如图是某城市一个主题雕塑的平面示意图,它由置放于地面l上两个半径均为2米的半圆与半径为4米的⊙A构成.点B、C分别是两个半圆的圆心,⊙A分别与两个半圆相切于点E、F,BC长为8米.求EF的长.
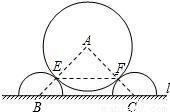
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(38):3.3 圆与圆的位置关系(解析版)
题型:解答题
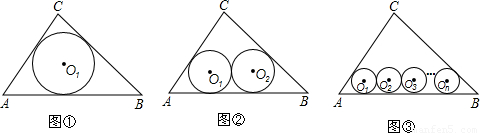
已知Rt△ABC中,∠ACB=90°,AC=6,BC=8.
(Ⅰ)如图①,若半径为r
1的⊙O
1是Rt△ABC的内切圆,求r
1;
(Ⅱ)如图②,若半径为r
2的两个等圆⊙O
1、⊙O
2外切,且⊙O
1与AC、AB相切,⊙O
2与BC、AB相切,求r
2;
(Ⅲ)如图③,当n大于2的正整数时,若半径r
n的n个等圆⊙O
1、⊙O
2、…、⊙O
n依次外切,且⊙O
1与AC、BC相切,⊙O
n与BC、AB相切,⊙O
1、⊙O
2、⊙O
3、…、⊙O
n-1均与AB边相切,求r
n.
查看答案和解析>>


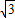 cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为t.
cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为t.
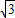 ,0),点M在⊙C上,并且∠BMO=120度.
,0),点M在⊙C上,并且∠BMO=120度.


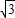 ≈1.73)
≈1.73)

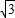 ≈1.73,结果精确到0.1mm)
≈1.73,结果精确到0.1mm)


