相关习题
0 128200 128208 128214 128218 128224 128226 128230 128236 128238 128244 128250 128254 128256 128260 128266 128268 128274 128278 128280 128284 128286 128290 128292 128294 128295 128296 128298 128299 128300 128302 128304 128308 128310 128314 128316 128320 128326 128328 128334 128338 128340 128344 128350 128356 128358 128364 128368 128370 128376 128380 128386 128394 366461
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(19):3.1 直线与圆的位置关系(解析版)
题型:解答题
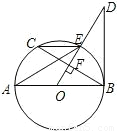
如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当AB=10,BC=8时,求BD的长.
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(19):3.1 直线与圆的位置关系(解析版)
题型:解答题
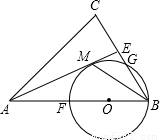
已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=

时,求⊙O的半径.
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(19):3.1 直线与圆的位置关系(解析版)
题型:解答题
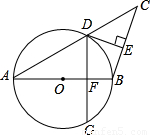
如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.
(1)求证:DE是⊙O的切线;
(2)作DG⊥AB交⊙O于G,垂足为F,若∠A=30°,AB=8,求弦DG的长.
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(19):3.1 直线与圆的位置关系(解析版)
题型:解答题
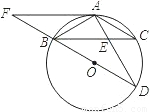
如图,⊙O是△ABC的外接圆,BD为圆O的直径,AB=AC,AD交BC于E,ED=2AE.
(1)求证:AB
2=AD•AE;
(2)求∠ADB的度数;
(3)延长DB到F,使BF=BO,连接FA.求证:直线FA为⊙O的切线.
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(19):3.1 直线与圆的位置关系(解析版)
题型:解答题
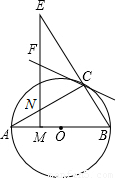
如图,AB是⊙O的直径,且点C为⊙O上的一点,∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且∠ECF=∠E.
(1)证明:CF是⊙O的切线;
(2)设⊙O的半径为1,且AC=CE,求MO的长.
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(19):3.1 直线与圆的位置关系(解析版)
题型:解答题
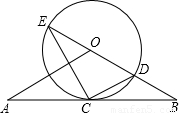
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
(1)求证:直线AB是⊙O的切线;
(2)试猜想BC,BD,BE三者之间的等量关系,并加以证明;
(3)若tan∠CED=

,⊙O的半径为3,求OA的长.
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(19):3.1 直线与圆的位置关系(解析版)
题型:解答题
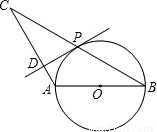
已知:如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点P,PD⊥AC于点D.
(1)求证:PD是⊙O的切线;
(2)若∠CAB=120°,AB=2,求BC的值.
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(19):3.1 直线与圆的位置关系(解析版)
题型:解答题
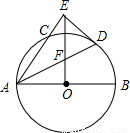
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
(1)求证:DE是⊙O的切线;
(2)若
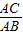
=

,求
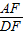
的值.
查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(19):3.1 直线与圆的位置关系(解析版)
题型:解答题
在Rt△ABC中,BC=9,CA=12,∠ABC的平分线BD交AC与点D,DE⊥DB交AB于点E.
(1)设⊙O是△BDE的外接圆,求证:AC是⊙O的切线;
(2)设⊙O交BC于点F,连接EF,求
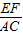
的值.

查看答案和解析>>
科目:
来源:第3章《直线与圆、圆与圆的位置关系》中考题集(19):3.1 直线与圆的位置关系(解析版)
题型:解答题
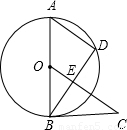
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.
(1)求证:BC是⊙O的切线;
(2)若BD=12,EC=10,求AD的长.
查看答案和解析>>


 已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径. 时,求⊙O的半径.
时,求⊙O的半径. 如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.
如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.

 ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.

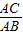 =
= ,求
,求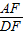 的值.
的值.
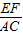 的值.
的值.
