
科目: 来源:第1章《解直角三角形》中考题集(26):1.3 解直角三角形(解析版) 题型:解答题
 x+4,直线BC与水平线BC1的交角为45度.
x+4,直线BC与水平线BC1的交角为45度.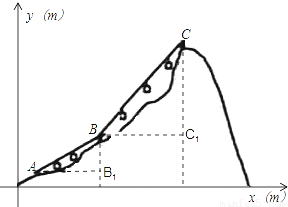
查看答案和解析>>
科目: 来源:第1章《解直角三角形》中考题集(26):1.3 解直角三角形(解析版) 题型:解答题
 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,-1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,-1)两点.
查看答案和解析>>
科目: 来源:第1章《解直角三角形》中考题集(26):1.3 解直角三角形(解析版) 题型:解答题
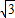 ),C(0,2
),C(0,2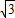 ),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S.
),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S.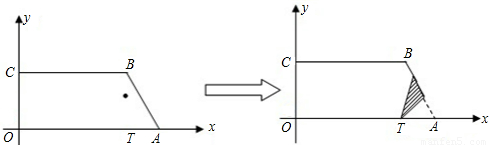
查看答案和解析>>
科目: 来源:第1章《解直角三角形》中考题集(26):1.3 解直角三角形(解析版) 题型:解答题
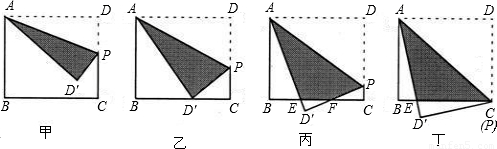
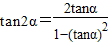 (α≠45°).根据上述阅读材料,求出用x表示y的解析式,并指出x的取值范围.
(α≠45°).根据上述阅读材料,求出用x表示y的解析式,并指出x的取值范围.查看答案和解析>>
科目: 来源:第1章《解直角三角形》中考题集(26):1.3 解直角三角形(解析版) 题型:解答题
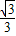 PQ;
PQ;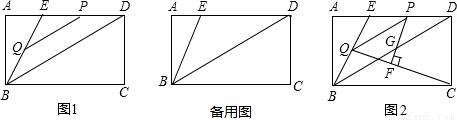
查看答案和解析>>
科目: 来源:第1章《解直角三角形》中考题集(26):1.3 解直角三角形(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第1章《解直角三角形》中考题集(26):1.3 解直角三角形(解析版) 题型:解答题
 AB长为半径画弧,两弧相交于点C、Q,连接CQ与AB相交于点D,连接AC,BC.那么:
AB长为半径画弧,两弧相交于点C、Q,连接CQ与AB相交于点D,连接AC,BC.那么:
查看答案和解析>>
科目: 来源:第1章《解直角三角形》中考题集(27):1.3 解直角三角形(解析版) 题型:解答题
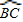 上任意一点.求证:PB+PC=PA;
上任意一点.求证:PB+PC=PA;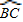 上任取一点P′,连接P′A、P′B、P′C、P′D.易知P′A+P′B+P′C=P′A+(P′B+P′C)=P′A+______;
上任取一点P′,连接P′A、P′B、P′C、P′D.易知P′A+P′B+P′C=P′A+(P′B+P′C)=P′A+______;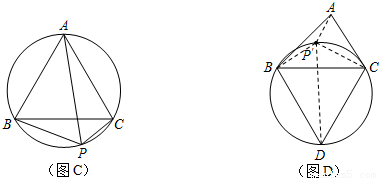
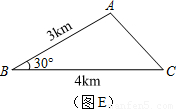
查看答案和解析>>
科目: 来源:第1章《解直角三角形》中考题集(27):1.3 解直角三角形(解析版) 题型:解答题
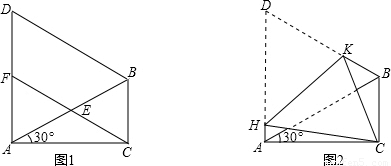
查看答案和解析>>
科目: 来源:第1章《解直角三角形》中考题集(27):1.3 解直角三角形(解析版) 题型:解答题
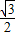 ,OP=2.
,OP=2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com