相关习题
0 128462 128470 128476 128480 128486 128488 128492 128498 128500 128506 128512 128516 128518 128522 128528 128530 128536 128540 128542 128546 128548 128552 128554 128556 128557 128558 128560 128561 128562 128564 128566 128570 128572 128576 128578 128582 128588 128590 128596 128600 128602 128606 128612 128618 128620 128626 128630 128632 128638 128642 128648 128656 366461
科目:
来源:第1章《解直角三角形》常考题集(15):1.3 解直角三角形(解析版)
题型:解答题
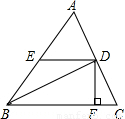
如图,在△ABC中,AC=15,BC=18,sinC=

,D是AC上一个动点(不运动至点A,C),过D作DE∥BC,交AB于E,过D作DF⊥BC,垂足为F,连接BD,设CD=x.
(1)用含x的代数式分别表示DF和BF;
(2)如果梯形EBFD的面积为S,求S关于x的函数关系式;
(3)如果△BDF的面积为S
1,△BDE的面积为S
2,那么x为何值时,S
1=2S
2.
查看答案和解析>>
科目:
来源:第1章《解直角三角形》常考题集(15):1.3 解直角三角形(解析版)
题型:解答题
已知在△ABC中,∠C=90°,
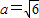
,
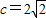
,解这个直角三角形.
查看答案和解析>>
科目:
来源:第1章《解直角三角形》常考题集(15):1.3 解直角三角形(解析版)
题型:解答题
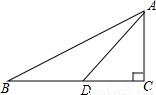
如图,在Rt△ABC中,∠C=90°,sinB=

,点D在BC边上,∠ADC=45°,DC=6,
求∠BAD的正切值.
查看答案和解析>>
科目:
来源:第1章《解直角三角形》常考题集(15):1.3 解直角三角形(解析版)
题型:解答题
如图1,一扇窗户打开后用窗钩AB可将其固定.
(1)这里所运用的几何原理是( )
(A)三角形的稳定性(B)两点之间线段最短;
(C)两点确定一条直线(D)垂线段最短;
(2)图2是图1中窗子开到一定位置时的平面图,若∠AOB=45°,∠OAB=30°,OA=60cm,求点B到OA边的距离.(
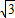
≈1.7,结果精确到整数)
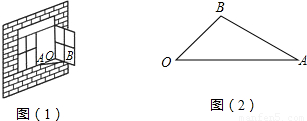
查看答案和解析>>
科目:
来源:第1章《解直角三角形》常考题集(15):1.3 解直角三角形(解析版)
题型:解答题
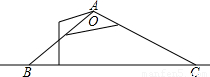
如图,一盏路灯沿灯罩边缘射出的光线与地面BC交于点B、C,测得∠ABC=45°,∠ACB=30°,且BC=20米.
(1)请用圆规和直尺画出路灯A到地面BC的距离AD;(不要求写出画法,但要保留作图痕迹)
(2)求出路灯A离地面的高度AD.(精确到0.1米)(参考数据:
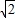
≈1.414,
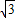
≈1.732).
查看答案和解析>>
科目:
来源:第1章《解直角三角形》常考题集(15):1.3 解直角三角形(解析版)
题型:解答题
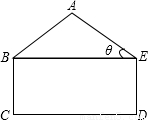
某工厂接受一批支援四川省汶川灾区抗震救灾帐篷的生产任务.根据要求,帐篷的一个横截面框架由等腰三角形和矩形组成(如图所示).已知等腰△ABE的底角∠AEB=θ,且tanθ=

,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m,求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
查看答案和解析>>
科目:
来源:第1章《解直角三角形》常考题集(15):1.3 解直角三角形(解析版)
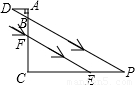
题型:解答题
如图,教室窗户的高度AF为2.5米,遮阳蓬外端一点D到窗户上椽的距离为AD,某一时刻太阳光从教室窗户射入室内,与地面的夹角∠BPC为30°,PE为窗户的一部分在教室地面所形成的影子且长为
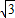
米,试求AD的长度.(结果带根号)
查看答案和解析>>
科目:
来源:第1章《解直角三角形》常考题集(15):1.3 解直角三角形(解析版)
题型:解答题
如图1、2,图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为5个单位(每个单位为5cm),设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=

.
(1)求点M离地面AC的高度BM(单位:厘米);
(2)设人站立点C与点A的水平距离AC等于11个单位,求铁环钩MF的长度(单位:厘
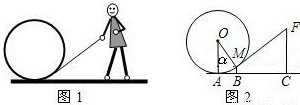
米).
查看答案和解析>>
科目:
来源:第1章《解直角三角形》常考题集(15):1.3 解直角三角形(解析版)
题型:解答题
如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.问:8秒后船向岸边移动了多少米?(结果精确到0.1米)
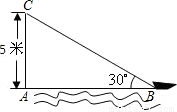
查看答案和解析>>
科目:
来源:第1章《解直角三角形》常考题集(15):1.3 解直角三角形(解析版)
题型:解答题
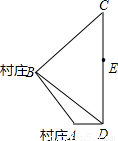
如图所示,A、B为两个村庄,AB、BC、CD为公路,BD为田地,AD为河宽,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一条电缆,共有如下两种铺设方案:
方案一:E?D?A?B;
方案二:E?C?B?A.
经测量得AB=4
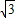
千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15度.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.
(1)求出河宽AD(结果保留根号);
(2)求出公路CD的长;
(3)哪种方案铺设电缆的费用低?请说明你的理由.
查看答案和解析>>

 ,D是AC上一个动点(不运动至点A,C),过D作DE∥BC,交AB于E,过D作DF⊥BC,垂足为F,连接BD,设CD=x.
,D是AC上一个动点(不运动至点A,C),过D作DE∥BC,交AB于E,过D作DF⊥BC,垂足为F,连接BD,设CD=x.
 ,点D在BC边上,∠ADC=45°,DC=6,
,点D在BC边上,∠ADC=45°,DC=6,
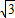 ≈1.7,结果精确到整数)
≈1.7,结果精确到整数)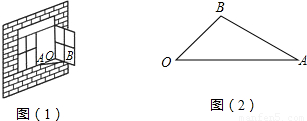
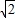 ≈1.414,
≈1.414,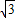 ≈1.732).
≈1.732).
 ,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m,求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m,求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
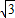 米,试求AD的长度.(结果带根号)
米,试求AD的长度.(结果带根号)
 .
. 米).
米).
 如图所示,A、B为两个村庄,AB、BC、CD为公路,BD为田地,AD为河宽,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一条电缆,共有如下两种铺设方案:
如图所示,A、B为两个村庄,AB、BC、CD为公路,BD为田地,AD为河宽,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一条电缆,共有如下两种铺设方案: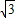 千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15度.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.
千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15度.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.