
科目: 来源:第1章《解直角三角形》常考题集(14):1.3 解直角三角形(解析版) 题型:解答题
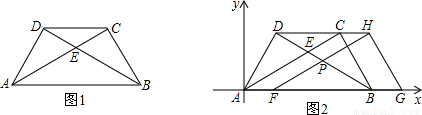
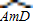 的长为底面周长的
的长为底面周长的 ,如图2所示.
,如图2所示.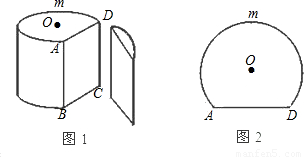
查看答案和解析>>
科目: 来源:第1章《解直角三角形》常考题集(14):1.3 解直角三角形(解析版) 题型:解答题
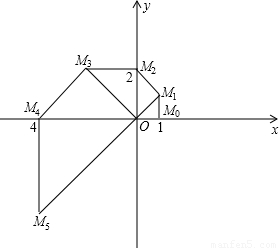
查看答案和解析>>
科目: 来源:第1章《解直角三角形》常考题集(14):1.3 解直角三角形(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第1章《解直角三角形》常考题集(14):1.3 解直角三角形(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第1章《解直角三角形》常考题集(14):1.3 解直角三角形(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第1章《解直角三角形》常考题集(14):1.3 解直角三角形(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第1章《解直角三角形》常考题集(14):1.3 解直角三角形(解析版) 题型:解答题
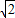 ,∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒.
,∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒.
查看答案和解析>>
科目: 来源:第1章《解直角三角形》常考题集(14):1.3 解直角三角形(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第1章《解直角三角形》常考题集(14):1.3 解直角三角形(解析版) 题型:解答题
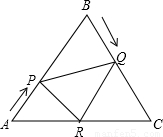
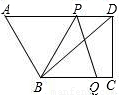
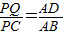 (如图1所示).
(如图1所示). ,且点Q在线段AB上时,设点B、Q之间的距离为x,
,且点Q在线段AB上时,设点B、Q之间的距离为x,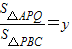 ,其中S△APQ表示△APQ的面积,S△PBC表示△PBC的面积,求y关于x的函数解析式,并写出函数定义域;
,其中S△APQ表示△APQ的面积,S△PBC表示△PBC的面积,求y关于x的函数解析式,并写出函数定义域;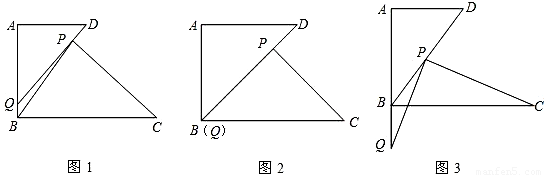
查看答案和解析>>
科目: 来源:第1章《解直角三角形》常考题集(14):1.3 解直角三角形(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com