相关习题
0 128922 128930 128936 128940 128946 128948 128952 128958 128960 128966 128972 128976 128978 128982 128988 128990 128996 129000 129002 129006 129008 129012 129014 129016 129017 129018 129020 129021 129022 129024 129026 129030 129032 129036 129038 129042 129048 129050 129056 129060 129062 129066 129072 129078 129080 129086 129090 129092 129098 129102 129108 129116 366461
科目:
来源:第26章《圆》中考题集(59):26.5 直线与圆的位置关系(解析版)
题型:解答题
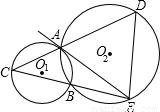
已知⊙O
1和⊙O
2相交于A、B两点,过A点作⊙O
1的切线交⊙O
2于点E,连接EB并延长交⊙O
1于点C,直线CA交⊙O
2于点D.
(1)如图,当点D与点A不重合时,试猜想线段EA=ED是否成立?证明你的结论;
(2)当点D与点A重合时,直线AC与⊙O
2有怎样的位置关系?此时若BC=2,CE=8,求⊙O
1的直径.
查看答案和解析>>
科目:
来源:第26章《圆》中考题集(59):26.5 直线与圆的位置关系(解析版)
题型:解答题
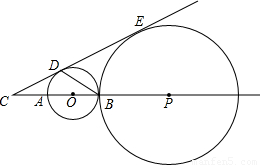
如图,AB是⊙O的直径,点C在BA的延长线上,CA=AO,点D在⊙O上,∠ABD=30°.
(1)求证:CD是⊙O的切线;
(2)若点P在直线AB上,⊙P与⊙O外切于点B,与直线CD相切于点E,设⊙O与⊙P的半径分别为r与R,求
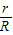
的值.
查看答案和解析>>
科目:
来源:第26章《圆》中考题集(59):26.5 直线与圆的位置关系(解析版)
题型:解答题
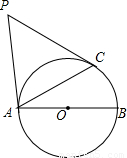
如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
(Ⅰ)求∠P的大小;
(Ⅱ)若AB=2,求PA的长(结果保留根号).
查看答案和解析>>
科目:
来源:第26章《圆》中考题集(59):26.5 直线与圆的位置关系(解析版)
题型:解答题
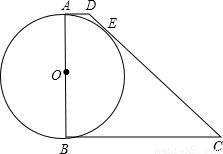
如图所示,在梯形ABCD中,AD∥BC,AB⊥BC,以AB为直径的⊙O与DC相切于E.已知AB=8,边BC比AD大6.
(1)求边AD、BC的长;
(2)在直径AB上是否存在一动点P,使以A、D、P为顶点的三角形与△BCP相似?若存在,求出AP的长;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第26章《圆》中考题集(59):26.5 直线与圆的位置关系(解析版)
题型:解答题
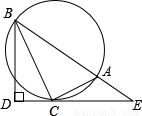
如图,Rt△BDE中,∠BDE=90°,BC平分∠DBE交DE于点C,AC⊥CB交BE于点A,△ABC的外接圆的半径为r.
(1)若∠E=30°,求证:BC•BD=r•ED;
(2)若BD=3,DE=4,求AE的长.
查看答案和解析>>
科目:
来源:第26章《圆》中考题集(59):26.5 直线与圆的位置关系(解析版)
题型:解答题
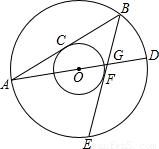
如图,两个同心圆的圆心是O,大圆的半径为13,小圆的半径为5,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.
(1)求BD的长;
(2)求∠ABE+2∠D的度数;
(3)求
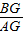
的值.
查看答案和解析>>
科目:
来源:第26章《圆》中考题集(59):26.5 直线与圆的位置关系(解析版)
题型:解答题
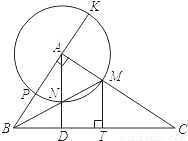
如图,在△ABC中,∠BAC=90度.BM平分∠ABC交AC于M,以A为圆心,AM为半径作⊙A交BM于N,AN的延长线交BC于D,直线AB交⊙A于P,K两点,作MT⊥BC于T.
(1)求证:AK=MT;
(2)求证:AD⊥BC;
(3)当AK=BD时,求证:
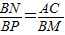
.
查看答案和解析>>
科目:
来源:第26章《圆》中考题集(61):26.5 直线与圆的位置关系(解析版)
题型:解答题
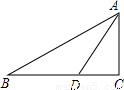
如图,在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.
(1)在图中作出⊙O(不写作法,保留作图痕迹);
(2)求证:BC为⊙O的切线;
(3)若AC=3,tanB=

,求⊙O的半径长.
查看答案和解析>>
科目:
来源:第26章《圆》中考题集(61):26.5 直线与圆的位置关系(解析版)
题型:解答题
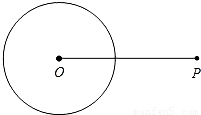
如图,已知⊙O及⊙O外的一点P.
(1)求作:过点P的⊙O的切线;
(要求:作图要利用直尺和圆规,不写作法,但要保留作图痕迹)
(2)若⊙O的半径为2,OP=6,求切线长.
查看答案和解析>>
科目:
来源:第26章《圆》中考题集(61):26.5 直线与圆的位置关系(解析版)
题型:解答题
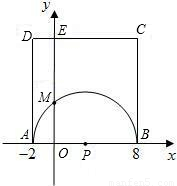
如图,在平面直角坐标系中,A,B两点的坐标分别为A(-2,0),B(8,0),以AB为直径的半圆与y轴交于点M,以AB为一边作正方形ABCD.
(1)求C,M两点的坐标;
(2)连接CM,试判断直线CM是否与⊙P相切?说明你的理由;
(3)在x轴上是否存在一点Q,使得△QMC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>


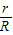 的值.
的值.



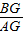 的值.
的值.
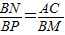 .
.
 ,求⊙O的半径长.
,求⊙O的半径长.

