
科目: 来源:第26章《圆》中考题集(08):26.1 旋转(解析版) 题型:解答题
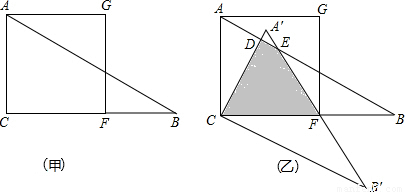
查看答案和解析>>
科目: 来源:第26章《圆》中考题集(08):26.1 旋转(解析版) 题型:解答题
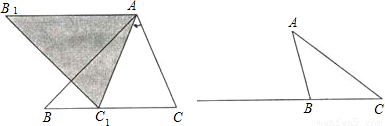
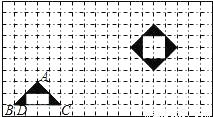 案”是如何通过“格点△ABC图案”变换得到的.
案”是如何通过“格点△ABC图案”变换得到的.查看答案和解析>>
科目: 来源:第26章《圆》中考题集(08):26.1 旋转(解析版) 题型:解答题
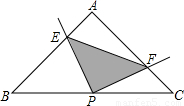
查看答案和解析>>
科目: 来源:第26章《圆》中考题集(08):26.1 旋转(解析版) 题型:解答题
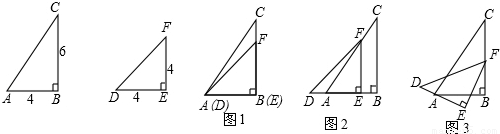
查看答案和解析>>
科目: 来源:第26章《圆》中考题集(08):26.1 旋转(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第26章《圆》中考题集(08):26.1 旋转(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第26章《圆》中考题集(08):26.1 旋转(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第26章《圆》中考题集(08):26.1 旋转(解析版) 题型:解答题
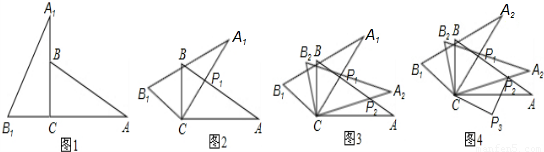
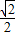 AP1;
AP1;查看答案和解析>>
科目: 来源:第26章《圆》中考题集(08):26.1 旋转(解析版) 题型:解答题
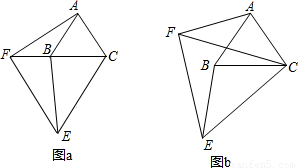 可),(1)中的结论还成立吗?作出判断不必说明理由;
可),(1)中的结论还成立吗?作出判断不必说明理由;查看答案和解析>>
科目: 来源:第26章《圆》中考题集(08):26.1 旋转(解析版) 题型:解答题
 ,-2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
,-2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.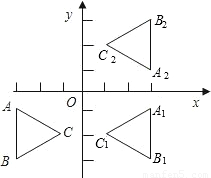
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com