
科目: 来源:第28章《锐角三角函数》中考题集(45):28.2 解直角三角形(解析版) 题型:解答题
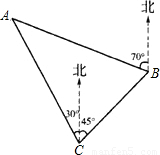
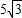 千米到达B地,然后再沿北偏西45°方向行进了5千米到达目的地点C.
千米到达B地,然后再沿北偏西45°方向行进了5千米到达目的地点C.
查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(45):28.2 解直角三角形(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(45):28.2 解直角三角形(解析版) 题型:解答题
 米的C处有一辆拖拉机以每秒8米的速度沿北偏东60°的方向CF行驶,若拖拉机的噪声污染半径为100米,试问A、B两栋教室是否受到拖拉机噪声的影响若有影响,影响的时间有多少秒?(计算过程中
米的C处有一辆拖拉机以每秒8米的速度沿北偏东60°的方向CF行驶,若拖拉机的噪声污染半径为100米,试问A、B两栋教室是否受到拖拉机噪声的影响若有影响,影响的时间有多少秒?(计算过程中 取1.7,各步计算结果精确到整数)
取1.7,各步计算结果精确到整数)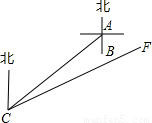
查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(45):28.2 解直角三角形(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(45):28.2 解直角三角形(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(45):28.2 解直角三角形(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(46):28.2 解直角三角形(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(46):28.2 解直角三角形(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(46):28.2 解直角三角形(解析版) 题型:解答题
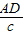 ,sinC=
,sinC=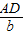 ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即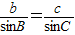 .
.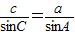 ,
,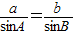 .
.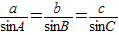 …(*)
…(*)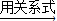 ______
______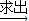 ∠B;
∠B;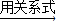 ______
______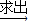 ∠C;
∠C;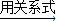 ______
______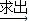 c.
c.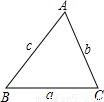
查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(46):28.2 解直角三角形(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com