科目： 来源：第28章《锐角三角函数》中考题集（40）：28.2 解直角三角形（解析版） 题型：解答题

已知：如图，有一飞行中的热气球，在A处时的热气球的探测器显示，从热气球看正前方一栋高楼顶部的仰角为45°，看这栋高楼底部的俯角为60°，热气球离地面的高度为150米，为了安全，避免热气球撞上高楼，请问热气球此时至少应再上升多少米？
（注：≈1.732，结果精确到1米）

科目： 来源：第28章《锐角三角函数》中考题集（40）：28.2 解直角三角形（解析版） 题型：解答题

如图，小明想测量塔BC的高度．他在楼底A处测得塔顶B的仰角为60°；爬到楼顶D处测得大楼AD的高度为18米，同时测得塔顶B的仰角为30°，求塔BC的高度．

科目： 来源：第28章《锐角三角函数》中考题集（40）：28.2 解直角三角形（解析版） 题型：解答题

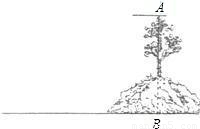
如图，小山上有一棵树．现有测角仪和皮尺两种测量工具，请你设计一种测量方案，在山脚水平地面上测出小树顶端A到水平地面的距离AB．
要求：
（1）画出测量示意图；
（2）写出测量步骤（测量数据用字母表示）；
（3）根据（2）中的数据计算AB．

科目： 来源：第28章《锐角三角函数》中考题集（40）：28.2 解直角三角形（解析版） 题型：解答题

兰州市城市规划期间，欲拆除黄河岸边的一根电线杆AB（如图），已知距电线杆AB水平距离14米处是河岸，即BD=14米，该河岸的坡面CD的坡角∠CDF的正切值为2，岸高CF为2米，在坡顶C处测得杆顶A的仰角为30°，D、E之间是宽2米的人行道，请你通过计算说明在拆除电线杆AB时，为确保安全，是否将此人行道封上？（在地面上以点B为圆心，以AB长为半径的圆形区域为危险区域）

科目： 来源：第28章《锐角三角函数》中考题集（40）：28.2 解直角三角形（解析版） 题型：解答题

如图，AB和CD是同一地面上的两座相距36米的楼房，在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°，楼底D的俯角为30度．求楼CD的高（结果保留根号）．

科目： 来源：第28章《锐角三角函数》中考题集（40）：28.2 解直角三角形（解析版） 题型：解答题

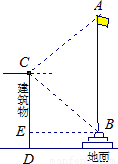
如图，张聪同学在学校某建筑物C点处测得旗杆顶部A的仰角为30°，旗杆底部B点的俯角为45°，若旗杆底部B点到该建筑物的水平距离BE=6米，旗杆台阶高1米，求旗杆顶部A离地面的高度．（结果保留根号）

科目： 来源：第28章《锐角三角函数》中考题集（41）：28.2 解直角三角形（解析版） 题型：解答题

如图，一枚运载火箭从地面O处发射，当火箭到达A点时，从地面C处的雷达站测得AC的距离是6km，仰角是43度．1s后，火箭到达B点，此时测得BC的距离是6.13km，仰角为45.54°，解答下列问题：
（1）火箭到达B点时距离发射点有多远？（精确到0.01km）
（2）火箭从A点到B点的平均速度是多少？（精确到0.1km/s）

科目： 来源：第28章《锐角三角函数》中考题集（41）：28.2 解直角三角形（解析版） 题型：解答题

如图，甲、乙两栋高楼的水平距离BD为90米，从甲楼顶部C点测得乙楼顶部A点的仰角α为30°，测得乙楼底部B点的俯角β为60°，求甲、乙两栋高楼各有多高？（计算过程和结果都不取近似值）

科目： 来源：第28章《锐角三角函数》中考题集（41）：28.2 解直角三角形（解析版） 题型：解答题

如图，线段AB，CD分别表示甲、乙两建筑物的高，AB⊥BC，CD⊥BC，从A点测得D点的俯角α为30°，测得C点的俯角β为60°，已知乙建筑物高CD=40米．试求甲建筑物高AB．

科目： 来源：第28章《锐角三角函数》中考题集（41）：28.2 解直角三角形（解析版） 题型：解答题

如图所示，某学校拟建两幢平行的教学楼，现设计两楼相距30米，从A点看C点，仰角为5°；从A点看D点，俯角为30°，解决下列问题：
（1）求两幢楼分别高多少米？（结果精确到1米）
（2）若冬日上午9：00太阳光的入射角最低为30°（光线与水平线的夹角），问一号楼的光照是否会有影响？请说明理由，若有，则两楼间距离应至少相距多少米时才会消除这种影响？（结果精确到1米）
（参考数据：tan5°≈0.0875，tan30°≈0.5774，cos30°≈1.732）