
科目: 来源:第28章《锐角三角函数》中考题集(35):28.2 解直角三角形(解析版) 题型:解答题
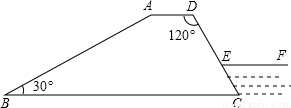
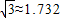 );
);查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(35):28.2 解直角三角形(解析版) 题型:解答题
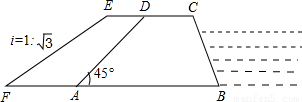
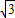 (i=1:
(i=1: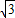 是指铅直高度DE与水平宽度CE的比),CD的长为10m,天桥另一斜面AB的坡角∠ABG=45°
是指铅直高度DE与水平宽度CE的比),CD的长为10m,天桥另一斜面AB的坡角∠ABG=45°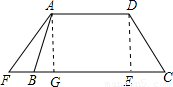
查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(35):28.2 解直角三角形(解析版) 题型:解答题
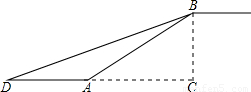
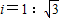 ,坡面AC长240米,南坡的坡角是45°.问李强以什么速度攀登才能和庞亮同时到达山顶A?(将山路AB、AC看成线段,结果保留根号)
,坡面AC长240米,南坡的坡角是45°.问李强以什么速度攀登才能和庞亮同时到达山顶A?(将山路AB、AC看成线段,结果保留根号)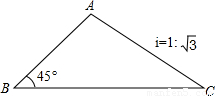
查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(35):28.2 解直角三角形(解析版) 题型:解答题
 =
=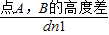 ;
;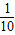 到
到 之间时,小明和小丁步行的平均速度均约为1.3米/秒;当坡度在
之间时,小明和小丁步行的平均速度均约为1.3米/秒;当坡度在 到
到 之间
之间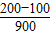 =
= ;
;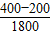 =
= ;
;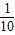 <
< <
< ,所以小明在路段AB,BP上步行的平均速度均约为1.3米/秒,因为
,所以小明在路段AB,BP上步行的平均速度均约为1.3米/秒,因为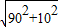 =906(米),斜坡BP的距离=
=906(米),斜坡BP的距离=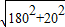 =1811(米),斜坡CP的距离=
=1811(米),斜坡CP的距离=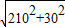 =2121(米),所以小明从家道学校的时间=
=2121(米),所以小明从家道学校的时间=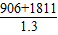 =2090(秒).小丁从家到学校的时间约为______秒.因此,______先到学校.
=2090(秒).小丁从家到学校的时间约为______秒.因此,______先到学校.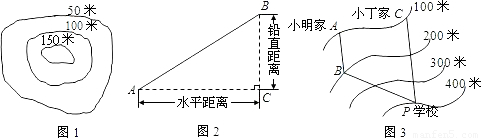
查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(35):28.2 解直角三角形(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(35):28.2 解直角三角形(解析版) 题型:解答题
 .
.
查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(35):28.2 解直角三角形(解析版) 题型:解答题
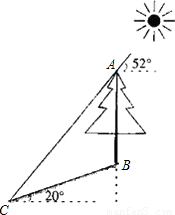
查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(35):28.2 解直角三角形(解析版) 题型:解答题
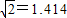 ,
,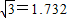 ,
,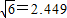 ,以上结果均保留到小数点后两位)
,以上结果均保留到小数点后两位)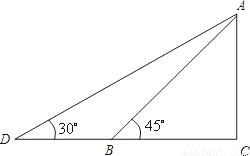
查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(35):28.2 解直角三角形(解析版) 题型:解答题
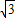 米,加固后大坝的横断面为梯形ABED.若CE的长为5米.
米,加固后大坝的横断面为梯形ABED.若CE的长为5米.
查看答案和解析>>
科目: 来源:第28章《锐角三角函数》中考题集(35):28.2 解直角三角形(解析版) 题型:解答题
 ,CD=10.
,CD=10.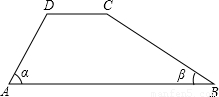
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com