相关习题
0 129199 129207 129213 129217 129223 129225 129229 129235 129237 129243 129249 129253 129255 129259 129265 129267 129273 129277 129279 129283 129285 129289 129291 129293 129294 129295 129297 129298 129299 129301 129303 129307 129309 129313 129315 129319 129325 129327 129333 129337 129339 129343 129349 129355 129357 129363 129367 129369 129375 129379 129385 129393 366461
科目:
来源:第28章《锐角三角函数》中考题集(33):28.2 解直角三角形(解析版)
题型:解答题
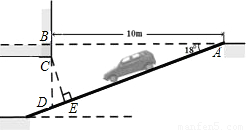
某商场为缓解我市“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说的对?请你判断并计算出正确的结果.(参考数据:sin18°=0.31,cos18°=0.95,tan18°=0.325)
(结果精确到0.1m)
查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(33):28.2 解直角三角形(解析版)
题型:解答题
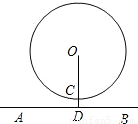
如图,是一个匀速旋转(指每分钟旋转的弧长或圆心角相同)的摩天轮的示意图,O为圆心,AB为水平地面,假设摩天轮的直径为80米,最低点C离地面为6米,旋转一周所用的时间为6分钟,小明从点C乘坐摩天轮(身高忽略不计),请问:
(1)经过2分钟后,小明离开地面的高度大约是多少米?
(2)若小明到了最高点,在视线没有阻挡的情况下能看到周围3公里远的地面景物,则他看到的地面景物有多大面积?(精确到1平方公里)
查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(33):28.2 解直角三角形(解析版)
题型:解答题
某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此太阳光线与地面成30°夹角.(
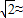
1.4,
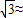
1.7)
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了

变化,假设太阳光线于地面夹角保持不变(用图(2)解答)
①求树与地面成45°角时的影长;
②求树的最大影长.
查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(33):28.2 解直角三角形(解析版)
题型:解答题
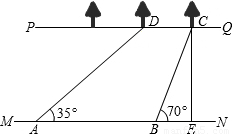
如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测得∠DAN=35°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CE(结果保留两个有效数字).
(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(33):28.2 解直角三角形(解析版)
题型:解答题
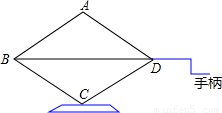
一种千斤顶利用了四边形的不稳定性.如图,其基本形状是一个菱形,中间通过螺杆连接,转动手柄可改变∠ADC的大小(菱形的边长不变),从而改变千斤顶的高度(即A、C之间的距离).若AB=40cm,当∠ADC从60°变为120°时,千斤顶升高了多少?(
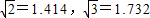
,结果保留整数)
查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(33):28.2 解直角三角形(解析版)
题型:解答题
为了测量学校旗杆AB的高度,学校数学实践小组做了如下实验:在阳光的照射下,旗杆AB的影子恰好落在水平地面BC的斜坡坡面CD上,测得BC=20m,CD=18m,太阳光线AD与水平面夹角为30°且与斜坡CD垂直.根据以上数据,请你求出旗杆AB的高度.(结果保留根号)
查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(33):28.2 解直角三角形(解析版)
题型:解答题
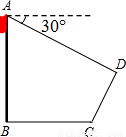
某市在举行“5.12汶川大地震”周年纪念活动时,根据地形搭建了一个台面为梯形(如图所示)的舞台,且台面铺设每平方米售价为a元的木板.已知AB=12米,AD=16米,∠B=60°,∠C=45°,计算购买铺设台面的木板所用资金是多少元?(不计铺设损耗,结果不取近似值)

查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(33):28.2 解直角三角形(解析版)
题型:解答题
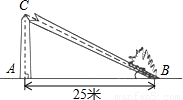
如图所示,一棵大树在一次强烈的地震中于C处折断倒下,树顶落在地面B处,测得B处与树的底端A相距25米,∠ABC=24度.
(1)求大树折断倒下部分BC的长度;(精确到1米)
(2)问大树在折断之前高多少米?(精确到1米)
查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(34):28.2 解直角三角形(解析版)
题型:解答题
如图1,一扇窗户打开后用窗钩AB可将其固定.
(1)这里所运用的几何原理是( )
(A)三角形的稳定性(B)两点之间线段最短;
(C)两点确定一条直线(D)垂线段最短;
(2)图2是图1中窗子开到一定位置时的平面图,若∠AOB=45°,∠OAB=30°,OA=60cm,求点B到OA边的距离.(
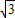
≈1.7,结果精确到整数)
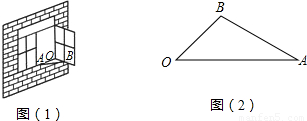
查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(34):28.2 解直角三角形(解析版)
题型:解答题
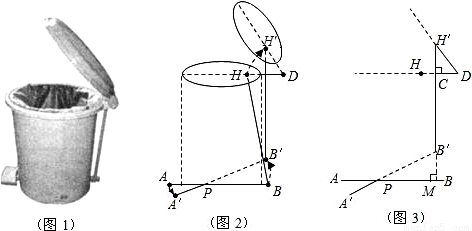
如图1,图2,是一款家用的垃圾桶,踏板AB(与地面平行)或绕定点P(固定在垃圾桶底部的某一位置)上下转动(转动过程中始终保持AP=A′P,BP=B′P).通过向下踩踏点A到A′(与地面接触点)使点B上升到点B′,与此同时传动杆BH运动到B'H'的位置,点H绕固定点D旋转(DH为旋转半径)至点H',从而使桶盖打开一个张角∠HDH′.如图3,桶盖打开后,传动杆H′B′所在的直线分别与水平直线AB、DH垂直,垂足为点M、C,设H′C=B′M.测得AP=6cm,PB=12cm,DH′=8cm.要使桶盖张开的角度∠HDH'不小于60°,那么踏板AB离地面的高度至少等于多少cm?(结果保留两位有效数字)(参考数据:
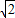
≈1.41,
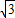
≈1.73)
查看答案和解析>>



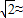 1.4,
1.4,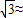 1.7)
1.7) 变化,假设太阳光线于地面夹角保持不变(用图(2)解答)
变化,假设太阳光线于地面夹角保持不变(用图(2)解答)
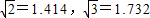 ,结果保留整数)
,结果保留整数)



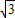 ≈1.7,结果精确到整数)
≈1.7,结果精确到整数)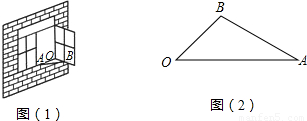
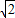 ≈1.41,
≈1.41,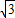 ≈1.73)
≈1.73)