相关习题
0 129245 129253 129259 129263 129269 129271 129275 129281 129283 129289 129295 129299 129301 129305 129311 129313 129319 129323 129325 129329 129331 129335 129337 129339 129340 129341 129343 129344 129345 129347 129349 129353 129355 129359 129361 129365 129371 129373 129379 129383 129385 129389 129395 129401 129403 129409 129413 129415 129421 129425 129431 129439 366461
科目:
来源:第28章《锐角三角函数》中考题集(12):28.1 锐角三角函数(解析版)
题型:解答题
如图,⊙O
1与⊙O
2外切于点P,外公切线AB切⊙O
1于点A,切⊙O
2于点B,
(1)求证:AP⊥BP;
(2)若⊙O
1与⊙O
2的半径分别为r和R,求证:
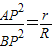
;
(3)延长AP交⊙O
2于C,连接BC,若r:R=2:3,求tan∠C的值.

查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(12):28.1 锐角三角函数(解析版)
题型:解答题
如图,已知AB是⊙O的弦,半径OA=2cm,∠AOB=120°.
(1)求tan∠OAB的值;
(2)计算S
△AOB;
(3)⊙O上一动点P从A点出发,沿逆时针方向运动,当S
△POA=S
△AOB时,求P点所经过的弧长.(不考虑点P与点B重合的情形)
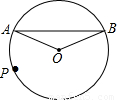
查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(13):28.1 锐角三角函数(解析版)
题型:解答题
如图,⊙O的半径等于1,弦AB和半径OC互相平分于点M.求扇形OACB的面积(结果保留π).
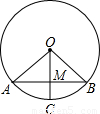
查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(13):28.1 锐角三角函数(解析版)
题型:解答题
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(13):28.1 锐角三角函数(解析版)
题型:解答题
如图,已知AB是⊙O的直径,点C在⊙O上,且AB=13,BC=5.
(1)求sin∠BAC的值;
(2)如果OD⊥AC,垂足为D,求AD的长;
(3)求图中阴影部分的面积.(精确到0.1)
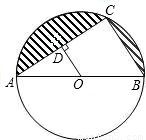
查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(13):28.1 锐角三角函数(解析版)
题型:解答题
在矩形ABCD中,AB=2,AD=
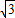
.
(1)在边CD上找一点E,使EB平分∠AEC,并加以说明;
(2)若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.
①求证:点B平分线段AF;
②△PAE能否由△PFB绕P点按顺时针方向旋转而得到?若能,加以证明,并求出旋转度数;若不能,请说明理由.

查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(13):28.1 锐角三角函数(解析版)
题型:解答题
如图,△ABC中,点D在AC上,点E在BC上,且DE∥AB,将△CDE绕点C按顺时针方向旋转得到△CD′E′(使∠BCE′<180°),连接AD′、BE′,设直线BE′与AC、AD′分别交于点O、E.
(1)若△ABC为等边三角形,则

的值为1,求∠AFB的度数;
(2)若△ABC满足∠ACB=60°,AC=

,BC=
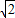
,①求

的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.

查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(13):28.1 锐角三角函数(解析版)
题型:解答题
在梯形ABCD中,AB∥CD,AD=BC,延长AB到E,使BE=CD,连接CE.
(1)求证:CE=CA;
(2)在上述条件下,若AF⊥CE于点F,且AF平分∠DAE,CD:AE=3:8,求cos∠ACF的值.

查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(13):28.1 锐角三角函数(解析版)
题型:解答题
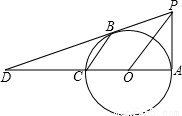
如图,已知:AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于D,BD=2PA.
(1)证明:直线PB是⊙O的切线;
(2)探究线段PO与线段BC之间的数量关系,并加以证明;
(3)求sin∠OPA的值.
查看答案和解析>>
科目:
来源:第28章《锐角三角函数》中考题集(13):28.1 锐角三角函数(解析版)
题型:解答题
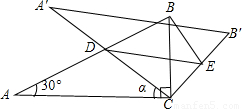
如图,将含30°角的直角三角板ABC(∠A=30°)绕其直角顶点C顺时针旋转α角(0°<α<90°),得到Rt△A′B′C,A′C与AB交于点D,过点D作DE∥A′B′交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.
(1)当α=30°时,求x的值.
(2)求S与x的函数关系式,并写出x的取值范围;
(3)以点E为圆心,BE为半径作⊙E,当S=

时,判断⊙E与A′C的位置关系,并求相应的tanα值.
查看答案和解析>>

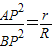 ;
;




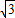 .
.
 的值为1,求∠AFB的度数;
的值为1,求∠AFB的度数; ,BC=
,BC=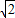 ,①求
,①求 的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.
的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.


 时,判断⊙E与A′C的位置关系,并求相应的tanα值.
时,判断⊙E与A′C的位置关系,并求相应的tanα值.