
科目: 来源:第27章《相似》中考题集(03):27.1 图形的相似(解析版) 题型:解答题
 成立.(考生不必证明)
成立.(考生不必证明) 还成立吗?
还成立吗?
查看答案和解析>>
科目: 来源:第27章《相似》中考题集(03):27.1 图形的相似(解析版) 题型:解答题
 ,因为DE=EP,所以DF=FC.可求出EF和EG的值,进而可求得EM与EN的比值.
,因为DE=EP,所以DF=FC.可求出EF和EG的值,进而可求得EM与EN的比值.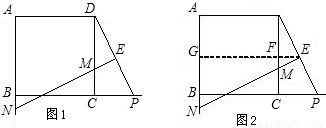
查看答案和解析>>
科目: 来源:第27章《相似》中考题集(03):27.1 图形的相似(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第27章《相似》中考题集(03):27.1 图形的相似(解析版) 题型:解答题
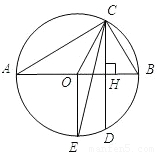 如图所示,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H.
如图所示,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H. ,求∠BAC的度数;
,求∠BAC的度数; 的中点,连接OE,CE.求证:CE平分∠OCD;
的中点,连接OE,CE.求证:CE平分∠OCD;查看答案和解析>>
科目: 来源:第27章《相似》中考题集(03):27.1 图形的相似(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第27章《相似》中考题集(03):27.1 图形的相似(解析版) 题型:解答题
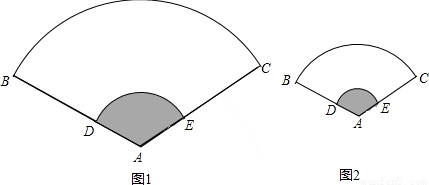
查看答案和解析>>
科目: 来源:第27章《相似》中考题集(03):27.1 图形的相似(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第27章《相似》中考题集(03):27.1 图形的相似(解析版) 题型:解答题
 秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
查看答案和解析>>
科目: 来源:第27章《相似》中考题集(03):27.1 图形的相似(解析版) 题型:解答题
 ,
,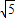 =2.236.
=2.236.
查看答案和解析>>
科目: 来源:第27章《相似》中考题集(03):27.1 图形的相似(解析版) 题型:解答题
 的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小波同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):
的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小波同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com