相关习题
0 129487 129495 129501 129505 129511 129513 129517 129523 129525 129531 129537 129541 129543 129547 129553 129555 129561 129565 129567 129571 129573 129577 129579 129581 129582 129583 129585 129586 129587 129589 129591 129595 129597 129601 129603 129607 129613 129615 129621 129625 129627 129631 129637 129643 129645 129651 129655 129657 129663 129667 129673 129681 366461
科目:
来源:第26章《二次函数》常考题集(23):26.3 实际问题与二次函数(解析版)
题型:解答题
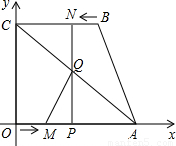
如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.
(1)点______(填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:
来源:第26章《二次函数》常考题集(23):26.3 实际问题与二次函数(解析版)
题型:解答题
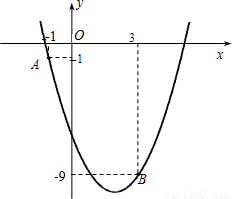
如图,已知二次函数y=ax
2-4x+c的图象经过点A和点B.
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离.
查看答案和解析>>
科目:
来源:第26章《二次函数》常考题集(23):26.3 实际问题与二次函数(解析版)
题型:解答题
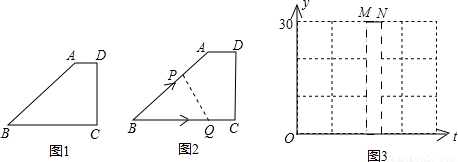
在直角梯形ABCD中,∠C=90°,高CD=6cm(如图1).动点P,Q同时从点B出发,点P沿BA,AD,DC运动到点C停止,点Q沿BC运动到C点停止.两点运动时的速度都是1cm/s.而当点P到达点A时,点Q正好到达点C.设P,Q同时从点B出发,经过的时间为t(s)时,△BPQ的面积为y(cm
2)(如图2).分别以x,y为横、纵坐标建立直角坐标系,已知点P在AD边上从A到D运动时,y与t的函数图象是图3中的线段MN.
(1)分别求出梯形中BA,AD的长度;
(2)写出图3中M,N两点的坐标;
(3)分别写出点P在BA边上和DC边上运动时,y与t的函数关系式(注明自变量的取值范围),并在答题卷的图4(放大了的图3)中补全整个运动中y关于t的函数关系的大致图象.
查看答案和解析>>
科目:
来源:第26章《二次函数》常考题集(23):26.3 实际问题与二次函数(解析版)
题型:解答题
在平面直角坐标系中,△AOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(-3,1).
(1)求点B的坐标;
(2)求过A,O,B三点的抛物线的解析式;
(3)设点B关于抛物线的对称轴l的对称点为B
1,求△AB
1B的面积.

查看答案和解析>>
科目:
来源:第26章《二次函数》常考题集(23):26.3 实际问题与二次函数(解析版)
题型:解答题
如图,一元二次方程x
2+2x-3=0的二根x
1,x
2(x
1<x
2)是抛物线y=ax
2+bx+c与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).
(1)求此二次函数的解析式;
(2)设此抛物线的顶点为P,对称轴与线段AC相交于点Q,求点P和点Q的坐标;
(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.
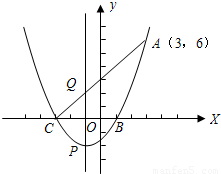
查看答案和解析>>
科目:
来源:第26章《二次函数》常考题集(23):26.3 实际问题与二次函数(解析版)
题型:解答题
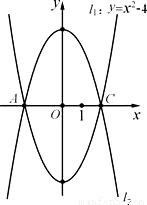
如图,已知抛物线l
1:y=x
2-4的图象与x轴相交于A、C两点,B是抛物线l
1上的动点(B不与A、C重合),抛物线l
2与l
1关于x轴对称,以AC为对角线的平行四边形ABCD的第四个顶点为D.
(1)求l
2的解析式;
(2)求证:点D一定在l
2上;
(3)?ABCD能否为矩形?如果能为矩形,求这些矩形公共部分的面积(若只有一个矩形符合条件,则求此矩形的面积);如果不能为矩形,请说明理由.
注:计算结果不取近似值.
查看答案和解析>>
科目:
来源:第26章《二次函数》常考题集(23):26.3 实际问题与二次函数(解析版)
题型:解答题
已知:m、n是方程x
2-6x+5=0的两个实数根,且m<n,抛物线y=-x
2+bx+c的图象经过点

A(m,0)、B(0,n).
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
查看答案和解析>>
科目:
来源:第26章《二次函数》常考题集(23):26.3 实际问题与二次函数(解析版)
题型:解答题
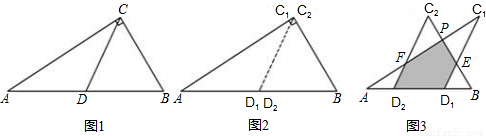
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC
1D
1和△BC
2D
2两个三角形(如图所示).将纸片△AC
1D
1沿直线D
2B(AB)方向平移(点A,D
1,D
2,B始终在同一直线上),当点D
1于点B重合时,停止平移.在平移过程中,C
1D
1与BC
2交于点E,AC
1与C
2D
2、BC
2分别交于点F、P.
(1)当△AC
1D
1平移到如图3所示的位置时,猜想图中的D
1E与D
2F的数量关系,并证明你的猜想;
(2)设平移距离D
2D
1为x,△AC
1D
1与△BC
2D
2重叠部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x的值使得y=

S
△ABC;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第26章《二次函数》常考题集(23):26.3 实际问题与二次函数(解析版)
题型:解答题

如图抛物线y=
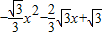
,x轴于A、B两点,交y轴于点C,顶点为D.
(1)求A、B、C的坐标;
(2)把△ABC绕AB的中点M旋转180°,得到四边形AEBC:
①求E点坐标;
②试判断四边形AEBC的形状,并说明理由;
(3)试探索:在直线BC上是否存在一点P,使得△PAD的周长最小?若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第26章《二次函数》常考题集(23):26.3 实际问题与二次函数(解析版)
题型:解答题
如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达B,C点),
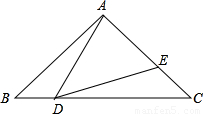
过D作∠ADE=45°,DE交AC于E.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数表达式;
(3)当△ADE是等腰三角形时,求AE的长.
查看答案和解析>>





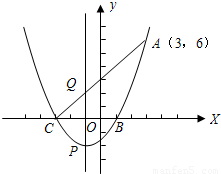

 A(m,0)、B(0,n).
A(m,0)、B(0,n). S△ABC;若不存在,请说明理由.
S△ABC;若不存在,请说明理由.
 如图抛物线y=
如图抛物线y=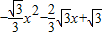 ,x轴于A、B两点,交y轴于点C,顶点为D.
,x轴于A、B两点,交y轴于点C,顶点为D. 过D作∠ADE=45°,DE交AC于E.
过D作∠ADE=45°,DE交AC于E.