科目： 来源：第26章《二次函数》常考题集（20）：26.3 实际问题与二次函数（解析版） 题型：解答题

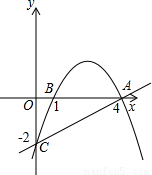
如图，已知直线y=x+1与y轴交于点A，与x轴交于点D，抛物线y=x²+bx+c与直线交于A、E两点，与x轴交于B、C两点，且B点坐标为（1，0）．
（1）求该抛物线的解析式；
（2）动点P在x轴上移动，当△PAE是直角三角形时，求点P的坐标P；
（3）在抛物线的对称轴上找一点M，使|AM-MC|的值最大，求出点M的坐标．

科目： 来源：第26章《二次函数》常考题集（20）：26.3 实际问题与二次函数（解析版） 题型：解答题

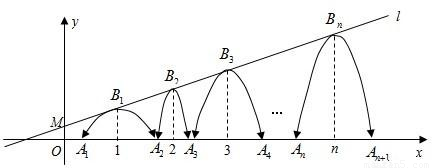
已知：如图，直线l：y=x+b，经过点M（0，），一组抛物线的顶点B₁（1，y₁），B₂（2，y₂），B₃（3，y₃），…，B_n（n，y_n）（n为正整数）依次是直线l上的点，这组抛物线与x轴正半轴的交点依次是：A₁（x₁，0），A₂（x₂，0），A₃（x₃，0），…A_n+1（x_n+1，0），设x₁=d（0＜d＜1）．
（1）求b的值；
（2）求经过点A₁、B₁、A₂的抛物线的解析式（用含d的代数式表示）；
（3）定义：若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形，则这种抛物线就称为：“美丽抛物线”．探究：当d（0＜d＜1）的大小变化时，这组抛物线中是否存在美丽抛物线？若存在，请你求出相应的d的值．

科目： 来源：第26章《二次函数》常考题集（20）：26.3 实际问题与二次函数（解析版） 题型：解答题

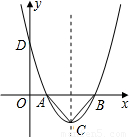
如图，抛物线经过A（4，0），B（1，0），C（0，-2）三点．
（1）求出抛物线的解析式；
（2）P是抛物线上一动点，过P作PM⊥x轴，垂足为M，是否存在P点，使得以A，P，M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；
（3）在直线AC上方的抛物线上有一点D，使得△DCA的面积最大，求出点D的坐标．

科目： 来源：第26章《二次函数》常考题集（20）：26.3 实际问题与二次函数（解析版） 题型：解答题

如图，已知抛物线y=x²+bx+c经过A（1，0），B（0，2）两点，顶点为D．
（1）求抛物线的解析式；
（2）将△OAB绕点A顺时针旋转90°后，点B落到点C的位置，将抛物线沿y轴平移后经过点C，求平移后所得图象的函数关系式；
（3）设（2）中平移后，所得抛物线与y轴的交点为B₁，顶点为D₁，若点N在平移后的抛物线上，且满足△NBB₁的面积是△NDD₁面积的2倍，求点N的坐标．

科目： 来源：第26章《二次函数》常考题集（20）：26.3 实际问题与二次函数（解析版） 题型：解答题

一开口向上的抛物线与x轴交于A（m-2，0），B（m+2，0）两点，记抛物线顶点为C，且AC⊥BC．
（1）若m为常数，求抛物线的解析式；
（2）若m为小于0的常数，那么（1）中的抛物线经过怎么样的平移可以使顶点在坐标原点；
（3）设抛物线交y轴正半轴于D点，问是否存在实数m，使得△BOD为等腰三角形？若存在，求出m的值；若不存在，请说明理由．

科目： 来源：第26章《二次函数》常考题集（20）：26.3 实际问题与二次函数（解析版） 题型：解答题

如图，抛物线y=-x²+2x+3与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．
（1）直接写出A、B、C三点的坐标和抛物线的对称轴；
（2）连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m；
①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PEDF为平行四边形？
②设△BCF的面积为S，求S与m的函数关系式．

科目： 来源：第26章《二次函数》常考题集（20）：26.3 实际问题与二次函数（解析版） 题型：解答题

如图，已知二次函数y=x²-2x-1的图象的顶点为A．二次函数y=ax²+bx的图象与x轴交于原点O及另一点C，它的顶点B在函数y=x²-2x-1的图象的对称轴上．
（1）求点A与点C的坐标；
（2）当四边形AOBC为菱形时，求函数y=ax²+bx的关系式．

科目： 来源：第26章《二次函数》常考题集（20）：26.3 实际问题与二次函数（解析版） 题型：解答题

如图，抛物线y=-x²+bx+c与x轴交于A（1，0），B（-3，0）两点．
（1）求该抛物线的解析式；
（2）设（1）中的抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由；
（3）在（1）中的抛物线上的第二象限上是否存在一点P，使△PBC的面积最大？若存在，求出点P的坐标及△PBC的面积最大值；若没有，请说明理由．

科目： 来源：第26章《二次函数》常考题集（20）：26.3 实际问题与二次函数（解析版） 题型：解答题

已知：抛物线y=ax²+bx+c（a≠0）的对称轴为x=-1，与x轴交于A，B两点，与y轴交于点C，其中A（-3，0），C（0，-2）
（1）求这条抛物线的函数表达式；
（2）已知在对称轴上存在一点P，使得△PBC的周长最小．请求出点P的坐标；
（3）若点D是线段OC上的一个动点（不与点O、点C重合）．过点D作DE∥PC交x轴于点E．连接PD、PE．设CD的长为m，△PDE的面积为S．求S与m之间的函数关系式．试说明S是否存在最大值？若存在，请求出最大值；若不存在，请说明理由．

科目： 来源：第26章《二次函数》常考题集（20）：26.3 实际问题与二次函数（解析版） 题型：解答题

如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（4，0）、C（8，0）、D（8，8）．抛物线y=ax²+bx过A、C两点．
（1）直接写出点A的坐标，并求出抛物线的解析式；
（2）动点P从点A出发．沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD向终点D运动．速度均为每秒1个单位长度，运动时间为t秒．过点P作PE⊥AB交AC于点E．
①过点E作EF⊥AD于点F，交抛物线于点G．当t为何值时，线段EG最长？
②连接EQ．在点P、Q运动的过程中，判断有几个时刻使得△CEQ是等腰三角形？请直接写出相应的t值．