相关习题
0 129560 129568 129574 129578 129584 129586 129590 129596 129598 129604 129610 129614 129616 129620 129626 129628 129634 129638 129640 129644 129646 129650 129652 129654 129655 129656 129658 129659 129660 129662 129664 129668 129670 129674 129676 129680 129686 129688 129694 129698 129700 129704 129710 129716 129718 129724 129728 129730 129736 129740 129746 129754 366461
科目:
来源:第26章《二次函数》中考题集(37):26.3 实际问题与二次函数(解析版)
题型:解答题
△ABC中,∠A,∠B,∠C的对边分别为a,b,c,抛物线y=x2-2ax+b2交x轴于两点M,N,交y轴于点P,其中M的坐标是(a+c,0).
(1)求证:△ABC是直角三角形;
(2)若S△MNP=3S△NOP,①求cosC的值;②判断△ABC的三边长能否取一组适当的值,使三角形MND(D为抛物线的顶点)是等腰直角三角形?如能,请求出这组值;如不能,请说明理由.
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(37):26.3 实际问题与二次函数(解析版)
题型:解答题
如图,已知抛物线P:y=ax
2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
| x | … | -3 | -2 | 1 | 2 | … |
| y | … | 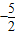 | -4 | 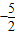 | | … |
(1)求A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=k•DF,若点M不在抛物线P上,求k的取值范围.

查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(37):26.3 实际问题与二次函数(解析版)
题型:解答题
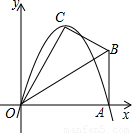
已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线y=ax
2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
注:抛物线y=ax
2+bx+c(a≠0)的顶点坐标为
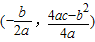
,对称轴公式为x=-
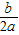
.
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(37):26.3 实际问题与二次函数(解析版)
题型:解答题
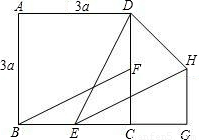
如图,正方形ABCD的边长为3a,两动点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,对应边EG=BC,B、E、C、G在一直线上.
(1)若BE=a,求DH的长;
(2)当E点在BC边上的什么位置时,△DHE的面积取得最小值?并求该三角形面积的最小值.
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(37):26.3 实际问题与二次函数(解析版)
题型:解答题
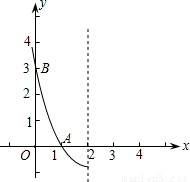
已知抛物线y=ax
2+bx+c的对称轴是经过点(2,0)且与y轴平行的直线,抛物线与x轴相交于点A(1,0),与y轴相交于点B(0,3),其在对称轴左侧的图象如图所示.
(1)求抛物线所对应的函数关系式,并写出抛物线的顶点坐标;
(2)画出抛物线在对称轴右侧的图象,并根据图象,写出当x为何值时,y<0.
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(37):26.3 实际问题与二次函数(解析版)
题型:解答题
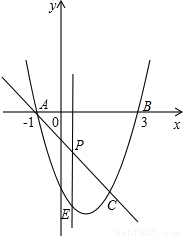
如图,抛物线y=x
2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(37):26.3 实际问题与二次函数(解析版)
题型:解答题
已知抛物线y=kx2-2kx+9-k(k为常数,k≠0),且当x>0时,y>1.
(1)求抛物线的顶点坐标;
(2)求k的取值范围;
(3)过动点P(0,n)作直线l⊥y轴,点O为坐标原点.
①当直线l与抛物线只有一个公共点时,求n关于k的函数关系式;
②当直线l与抛物线相交于A、B两点时,是否存在实数n,使得不论k在其取值范围内取任意值时,△AOB的面积为定值?如果存在,求出n的值;如果不存在,说明理由.
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(37):26.3 实际问题与二次函数(解析版)
题型:解答题
抛物线y=ax
2+bx+c交x轴于A,B两点,交y轴于点C,对称轴为直线x=1,已知:A(-1,0),C(0,-3).
(1)求抛物线y=ax
2+bx+c的解析式;
(2)求△AOC和△BOC的面积的比;
(3)在对称轴是否存在一个点P,使△PAC的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
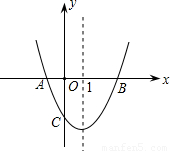
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(38):26.3 实际问题与二次函数(解析版)
题型:解答题
已知:如图,抛物线y=ax
2+bx+c经过A(1,0)、B(5,0)、C(0,5)三点.
(1)求抛物线的函数关系式;
(2)若过点C的直线y=kx+b与抛物线相交于点E(4,m),请求出△CBE的面积S的值;
(3)在抛物线上求一点P
,使得△ABP
为等腰三角形,并写出P
点的坐标;
附加:(4)除(3)中所求的P
点外,在抛物线上是否还存在其它的点P使得△ABP为等腰三角形?若存在,请求出一共有几个满足条件的点P(要求简要说明理由,但不证明);若不存在这样的点P,请说明理由.
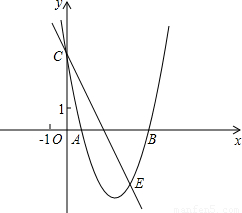
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(38):26.3 实际问题与二次函数(解析版)
题型:解答题
已知:直线y=x+6交x、y轴于A、C两点,经过A、O两点的抛物线y=ax
2+bx(a<0)的顶点在直线AC上.
(1)求A、C两点的坐标;
(2)求出抛物线的函数关系式;
(3)以B点为圆心,以AB为半径作⊙B,将⊙B沿x轴翻折得到⊙D,试判断直线AC与⊙D的位置关系,并求出BD的长;
(4)若E为⊙B劣弧OC上一动点,连接AE、OE,问在抛物线上是否存在一点M,使∠MOA:∠AEO=2:3?若存在,试求出点M的坐标;若不存在,试说明理由.
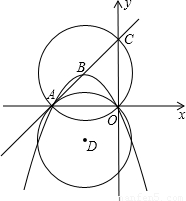
查看答案和解析>>

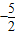
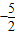

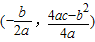 ,对称轴公式为x=-
,对称轴公式为x=-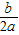 .
.


 如图,抛物线y=x2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
如图,抛物线y=x2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.

