相关习题
0 129565 129573 129579 129583 129589 129591 129595 129601 129603 129609 129615 129619 129621 129625 129631 129633 129639 129643 129645 129649 129651 129655 129657 129659 129660 129661 129663 129664 129665 129667 129669 129673 129675 129679 129681 129685 129691 129693 129699 129703 129705 129709 129715 129721 129723 129729 129733 129735 129741 129745 129751 129759 366461
科目:
来源:第26章《二次函数》中考题集(36):26.3 实际问题与二次函数(解析版)
题型:解答题
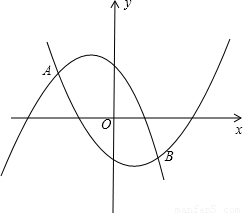
如图,抛物线y
1=-ax
2-ax+1经过点P(-

,

),且与抛物线y
2=ax
2-ax-1相交于A,B两点.
(1)求a值;
(2)设y
1=-ax
2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y
2=ax
2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为x
A,x
B,若在x轴上有一动点Q(x,0),且x
A≤x≤x
B,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(36):26.3 实际问题与二次函数(解析版)
题型:解答题
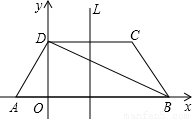
如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4.以AB所在直线为x轴,过D且垂直于AB的直线为y轴建立平面直角坐标系.
(1)求∠DAB的度数及A、D、C三点的坐标;
(2)求过A、D、C三点的抛物线的解析式及其对称轴L;
(3)若P是抛物线的对称轴L上的点,那么使△PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(36):26.3 实际问题与二次函数(解析版)
题型:解答题
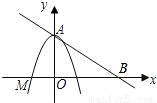
如图,在平面直角坐标系内,以y轴为对称轴的抛物线经过直y=-
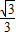
x+2与y轴的交点A和点M(-
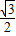
,0).
(1)求这条抛物线所对应的二次函数的关系式;
(2)将(1)中所求抛物线沿x轴向右平移.①在题目所给的图中画出沿x轴平移后经过原点的抛物线大致图象;②设沿x轴向右平移后经过原点的抛物线对称轴与直线AB相交于C点.判断以O为圆心,OC为半径的圆与直线AB的位置关系,并说明理由;
(3)P点是沿x轴向右平移后经过原点的抛物线对称轴上的点,求P点的坐标,使得以O,A,C,P四点为顶点的四边形是平行四边形.
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(36):26.3 实际问题与二次函数(解析版)
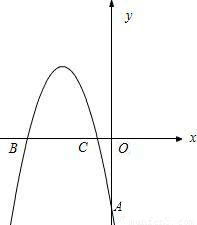
题型:解答题
如图,在平面直角坐标系中,抛物线y=-

x
2+bx+c经过A(0,-4)、B(x
1,0)、C(x
2,0)三点,且x
2-x
1=5.
(1)求b、c的值;
(2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;
(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(36):26.3 实际问题与二次函数(解析版)
题型:解答题
已知抛物线M:y=-x
2+2mx+n(m,n为常数,且m>0,n>0)的顶点为A,与y轴交于点C;抛物线N与抛物线M关于y轴对称,其顶点为B,连接AC,BC,AB.
问抛物线M上是否存在点P,使得四边形ABCP为菱形?如果存在,请求出m的值;如果不存在,请说明理由.
说明:
(1)如果你反复探索,没有解决问题,请写出探索过程(要求至少写3步);
(2)在你完成(1)之后,可以从①、②中选取一个条件,完成解答(选取①得7分;选取②得10分).
①n=1;②n=2.

查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(36):26.3 实际问题与二次函数(解析版)
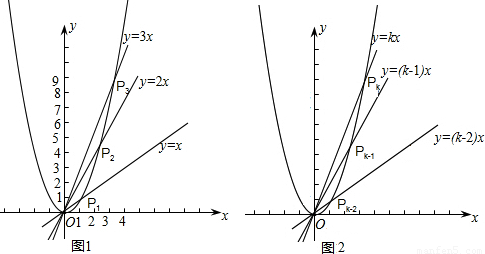
题型:解答题
如图1,P
1、P
2、P
3、…、P
n分别是抛物线y=x
2与直线y=x、y=2x、y=3x、…、y=kx的交点,连接P
1P
2、P
2P
3,…,P
k-1P
k.
(1)求△OP
1P
2的面积,并直接写出△OP
2P
3的面积;
(2)如图2,猜想△OP
k-1P
k的面积,并说明理由;
(3)若将抛物线y=x
2改为抛物线y=ax
2,其它条件不变,猜想△OP
k-1P
k的面积(直接写出答案).
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(36):26.3 实际问题与二次函数(解析版)
题型:解答题
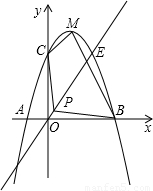
如图,已知二次函数y=ax
2+bx+c的图象经过三点A(-1,0),B(3,0),C(0,3),它的顶点为M,又正比例函数y=kx的图象于二次函数相交于两点D、E,且P是线段DE的中点.
(1)求该二次函数的解析式,并求函数顶点M的坐标;
(2)已知点E(2,3),且二次函数的函数值大于正比例函数时,试根据函数图象求出符合条件的自变量x的取值范围;
(3)0<k<2时,求四边形PCMB的面积s的最小值.
【参考公式:已知两点D(x
1,y
1),E(x
2,y
2),则线段DE的中点坐标为
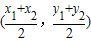
】
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(36):26.3 实际问题与二次函数(解析版)
题型:解答题
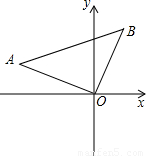
在平面直角坐标系中,△AOB的位置如图所示.已知∠AOB=90°,AO=BO,点A的坐标为(-3,1).
(1)求点B的坐标.
(2)求过A,O,B三点的抛物线的解析式.
(3)设点B关于抛物线的对称轴?的对称点为B
l,连接AB
1,求tan∠AB
1B的值.
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(36):26.3 实际问题与二次函数(解析版)
题型:解答题
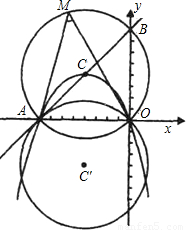
如图,已知直线y=x+8交x轴于A点,交y轴于B点,过A、0两点的抛物线y=ax
2+bx(a<O)的顶点C在直线AB上,以C为圆心,CA的长为半径作⊙C.
(1)求抛物线的对称轴、顶点坐标及解析式;
(2)将⊙C沿x轴翻折后,得到⊙C′,求证:直线AC是⊙C′的切线;
(3)若M点是⊙C的优弧
(不与0、A重合)上的一个动点,P是抛物线上的点,且∠POA=∠AM0,求满足条件的P点的坐标.
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(36):26.3 实际问题与二次函数(解析版)
题型:解答题
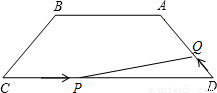
如图,等腰梯形ABCD中,AB=4,CD=9,∠C=60°,动点P从点C出发沿CD方向向点D运动,动点Q同时以相同速度从点D出发沿DA方向向终点A运动,其中一个动点到达端点时,另一个动点也随之停止运动.
(1)求AD的长;
(2)设CP=x,问当x为何值时△PDQ的面积达到最大,并求出最大值;
(3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由.
查看答案和解析>>

 ,
, ),且与抛物线y2=ax2-ax-1相交于A,B两点.
),且与抛物线y2=ax2-ax-1相交于A,B两点.

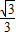 x+2与y轴的交点A和点M(-
x+2与y轴的交点A和点M(-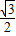 ,0).
,0).
 x2+bx+c经过A(0,-4)、B(x1,0)、C(x2,0)三点,且x2-x1=5.
x2+bx+c经过A(0,-4)、B(x1,0)、C(x2,0)三点,且x2-x1=5.


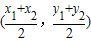 】
】

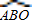 (不与0、A重合)上的一个动点,P是抛物线上的点,且∠POA=∠AM0,求满足条件的P点的坐标.
(不与0、A重合)上的一个动点,P是抛物线上的点,且∠POA=∠AM0,求满足条件的P点的坐标.
