相关习题
0 129590 129598 129604 129608 129614 129616 129620 129626 129628 129634 129640 129644 129646 129650 129656 129658 129664 129668 129670 129674 129676 129680 129682 129684 129685 129686 129688 129689 129690 129692 129694 129698 129700 129704 129706 129710 129716 129718 129724 129728 129730 129734 129740 129746 129748 129754 129758 129760 129766 129770 129776 129784 366461
科目:
来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版)
题型:解答题
某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加x元.求:
(1)房间每天的入住量y(间)关于x(元)的函数关系式;
(2)该宾馆每天的房间收费z(元)关于x(元)的函数关系式;
(3)该宾馆客房部每天的利润w(元)关于x(元)的函数关系式;当每个房间的定价为每天多少元时,w有最大值?最大值是多少?
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版)
题型:解答题
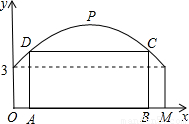
如图,某隧道横截面的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数解析式;
(3)若要搭建一个矩形“支撑架”AD+DC+CB,使C、D点在抛物线上,A、B点在地面OM上,这个“支撑架”总长的最大值是多少?
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版)
题型:解答题
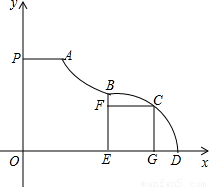
“假日旅乐园”中一种新型水上滑梯如图,其中线段PA表示距离水面(x轴)高度为5m的平台(点P在y轴上).滑道AB可以看作反比例函数图象的一部分,滑道BCD可以看作是二次函数图象的一部分,两滑道的连接点B为抛物线BCD的顶点,且点B到水面的距离BE=2m,点B到y轴的距离是5m.当小明从上而下滑到点C时,与水面的距离CG=

m,与点B的水平距离CF=2m.
(1)求反比例函数的解析式及其自变量的取值范围.
(2)求二次函数的解析式及其自变量的取值范围.
(3)小明从点B滑水面上点D处时,试求他所滑过的水平距离d.
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版)
题型:解答题
为了落实国务院副总理李克强同志到恩施考察时的指示精神,最近,州委州政府又出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w(千克)与销售价x(元/千克)有如下关系:w=-2x+80.设这种产品每天的销售利润为y(元).
(1)求y与x之间的函数关系式;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版)
题型:解答题
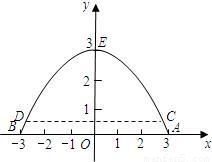
如图,河上有一座抛物线桥洞,已知桥下的水面离桥拱顶部3m时,水面宽AB为6m,当水位上升0.5m时:
(1)求水面的宽度CD为多少米?
(2)有一艘游船,它的左右两边缘最宽处有一个长方体形状的遮阳棚,此船正对着桥洞在上述河流中航行.
①若游船宽(指船的最大宽度)为2m,从水面到棚顶的高度为1.8m,问这艘游船能否从桥洞下通过?
②若从水面到棚顶的高度为

m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版)
题型:解答题
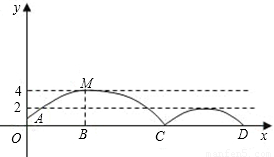
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点C距守门员多少米?(取4
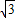
=7)
(3)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取
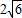
=5)
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版)
题型:解答题
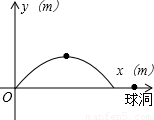
王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=-

x
2+

x,其中y(m)是球的飞行高度,x(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
(1)请写出抛物线的开口方向,顶点坐标,对称轴.
(2)请求出球飞行的最大水平距离.
(3)若王强再一次从此处击球,要想让球飞行的最大高度不变且球刚好进洞,则球飞行路线应满足怎样的抛物线,求出其解析式.
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版)
题型:解答题
杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(
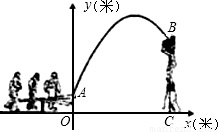
看成一点)的路线是抛物线y=
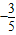
x
2+3x+1的一部分,如图所示.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版)
题型:解答题
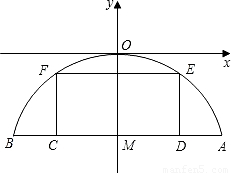
有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
(1)求此抛物线的解析式;
(2)如果限定矩形的长CD为9米,那么矩形的高DE不能超过多少米,才能使船通过拱桥;
(3)若设EF=a,请将矩形CDEF的面积S用含a的代数式表示,并指出a的取值范围.
查看答案和解析>>
科目:
来源:第26章《二次函数》中考题集(23):26.3 实际问题与二次函数(解析版)
题型:解答题
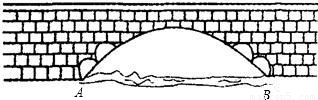
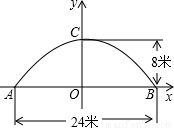
如图所示是永州八景之一的愚溪桥,桥身横跨愚溪,面临潇水,桥下冬暖夏凉,常有渔船停泊桥下避晒纳凉.已知主桥拱为抛物线型,在正常水位下测得主拱宽24m,最高点离水面8m,以水平线AB为x轴,24m的中点为原点建立坐标系.
①求此桥拱线所在抛物线的解析式;
②桥边有一浮在水面部分高4m,最宽处12
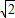
m的河鱼餐船,试探索此船能否开到桥下?说明理由.
查看答案和解析>>


 “假日旅乐园”中一种新型水上滑梯如图,其中线段PA表示距离水面(x轴)高度为5m的平台(点P在y轴上).滑道AB可以看作反比例函数图象的一部分,滑道BCD可以看作是二次函数图象的一部分,两滑道的连接点B为抛物线BCD的顶点,且点B到水面的距离BE=2m,点B到y轴的距离是5m.当小明从上而下滑到点C时,与水面的距离CG=
“假日旅乐园”中一种新型水上滑梯如图,其中线段PA表示距离水面(x轴)高度为5m的平台(点P在y轴上).滑道AB可以看作反比例函数图象的一部分,滑道BCD可以看作是二次函数图象的一部分,两滑道的连接点B为抛物线BCD的顶点,且点B到水面的距离BE=2m,点B到y轴的距离是5m.当小明从上而下滑到点C时,与水面的距离CG= m,与点B的水平距离CF=2m.
m,与点B的水平距离CF=2m. m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?
m的游船刚好能从桥洞下通过,则这艘游船的最大宽度是多少米?
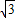 =7)
=7)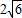 =5)
=5)
 x2+
x2+ x,其中y(m)是球的飞行高度,x(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
x,其中y(m)是球的飞行高度,x(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
 看成一点)的路线是抛物线y=
看成一点)的路线是抛物线y=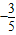 x2+3x+1的一部分,如图所示.
x2+3x+1的一部分,如图所示.
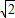 m的河鱼餐船,试探索此船能否开到桥下?说明理由.
m的河鱼餐船,试探索此船能否开到桥下?说明理由.
