
科目: 来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版) 题型:解答题
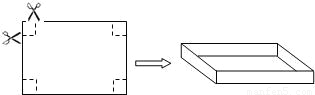
查看答案和解析>>
科目: 来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版) 题型:解答题
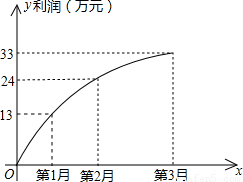
查看答案和解析>>
科目: 来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版) 题型:解答题
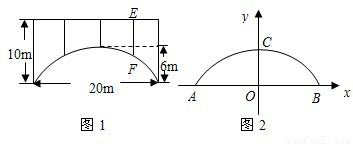
查看答案和解析>>
科目: 来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版) 题型:解答题
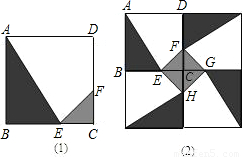
查看答案和解析>>
科目: 来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版) 题型:解答题
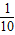 x2+5x+90,投入市场后当年能全部售出,且在甲、乙两地每吨的售价p甲,p乙(万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用)
x2+5x+90,投入市场后当年能全部售出,且在甲、乙两地每吨的售价p甲,p乙(万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用) x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润W甲(万元)与x之间的函数关系式;
x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润W甲(万元)与x之间的函数关系式;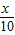 +n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值;
+n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值;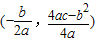 .
.查看答案和解析>>
科目: 来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第26章《二次函数》中考题集(22):26.3 实际问题与二次函数(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com