
科目: 来源:2008-2009学年吉林省长春市南关区九年级(下)期中联赛题(第22章至第27章)(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:2008-2009学年吉林省长春市南关区九年级(下)期中联赛题(第22章至第27章)(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:2008-2009学年吉林省长春市南关区九年级(下)期中联赛题(第22章至第27章)(解析版) 题型:解答题
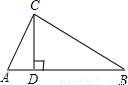
查看答案和解析>>
科目: 来源:2008-2009学年吉林省长春市南关区九年级(下)期中联赛题(第22章至第27章)(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:2008-2009学年吉林省长春市南关区九年级(下)期中联赛题(第22章至第27章)(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:2008-2009学年吉林省长春市南关区九年级(下)期中联赛题(第22章至第27章)(解析版) 题型:解答题
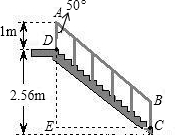
查看答案和解析>>
科目: 来源:2008-2009学年吉林省长春市南关区九年级(下)期中联赛题(第22章至第27章)(解析版) 题型:解答题
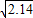 ≈1.463,
≈1.463,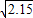 ≈1.466,
≈1.466,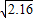 ≈1.470,
≈1.470,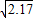 ≈1.473)
≈1.473)
查看答案和解析>>
科目: 来源:2008-2009学年吉林省长春市南关区九年级(下)期中联赛题(第22章至第27章)(解析版) 题型:解答题
 x(x≥0),射线OA上有一点M(8,y),另一点P从O点出发沿射线OA方向以每秒1个单位长度的速度运动,设运动时间为t秒,∠AOx=α.
x(x≥0),射线OA上有一点M(8,y),另一点P从O点出发沿射线OA方向以每秒1个单位长度的速度运动,设运动时间为t秒,∠AOx=α.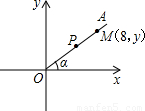
查看答案和解析>>
科目: 来源:2008-2009学年吉林省长春市南关区九年级(下)期中联赛题(第22章至第27章)(解析版) 题型:解答题
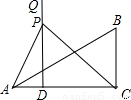
查看答案和解析>>
科目: 来源:2008-2009学年吉林省长春市南关区九年级(下)期中联赛题(第22章至第27章)(解析版) 题型:解答题
 时点P的坐标.
时点P的坐标.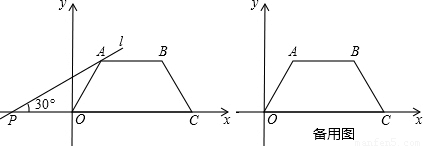
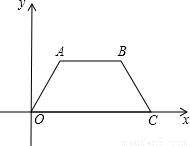
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com