相关习题
0 130458 130466 130472 130476 130482 130484 130488 130494 130496 130502 130508 130512 130514 130518 130524 130526 130532 130536 130538 130542 130544 130548 130550 130552 130553 130554 130556 130557 130558 130560 130562 130566 130568 130572 130574 130578 130584 130586 130592 130596 130598 130602 130608 130614 130616 130622 130626 130628 130634 130638 130644 130652 366461
科目:
来源:2012-2013学年新人教版九年级(上)期中数学试卷(4)(解析版)
题型:解答题
已知关于x的一元二次方程x2+2(k-1)x+k2-1=0有两个不相等的实数根.
(1)求实数k的取值范围;
(2)0可能是方程的一个根吗?若是,请求出它的另一个根;若不是,请说明理由.
查看答案和解析>>
科目:
来源:2012-2013学年新人教版九年级(上)期中数学试卷(4)(解析版)
题型:解答题
如图,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB、BC、CD、DA的中点分别为P、Q、M、N,试判断四边形PQMN为怎样的四边形,并证明你的结论.
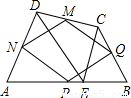
查看答案和解析>>
科目:
来源:2012-2013学年新人教版九年级(上)期中数学试卷(4)(解析版)
题型:解答题
查看答案和解析>>
科目:
来源:2012-2013学年新人教版九年级(上)期中数学试卷(4)(解析版)
题型:解答题
如图.矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的而积为
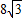
,求AC的长.
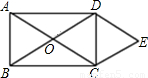
查看答案和解析>>
科目:
来源:2012-2013学年新人教版九年级(上)期中数学试卷(4)(解析版)
题型:解答题
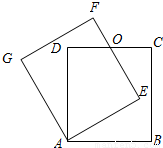
如图,正方形ABCD绕点A逆时针旋转n°后得到正方形AEFG,边EF与CD交于点O.
(1)以图中已标有字母的点为端点连接两条线段(正方形的对角线除外),要求所连接的两条线段相交且互相垂直,并说明这两条线段互相垂直的理由;
(2)若正方形的边长为2cm,重叠部分(四边形AEOD)的面积为
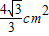
,求旋转的角度n.
查看答案和解析>>
科目:
来源:2012-2013学年新人教版九年级(上)期中数学试卷(4)(解析版)
题型:解答题
随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多地进入普通家庭,成为居民消费新的增长点.据某市交通部门统计,2008年底全市汽车拥有量为15万辆,而截止到2010年底,全市的汽车拥有量已达21.6万辆.
(1)求2008年底至2010年底该市汽车拥有量的年平均增长率;
(2)为保护城市环境,缓解汽车拥堵状况,从2011年初起,该市交通部门拟控制汽车总量,要求到2012年底全市汽车拥有量不超过23.196万辆;另据估计,该市从2011年起每年报废的汽车数量是上年底汽车拥有量的10%.假定在这种情况下每年新增汽车数量相同,请你计算出该市每年新增汽车数多不能超过多少万辆.
查看答案和解析>>
科目:
来源:2012-2013学年新人教版九年级(上)期中数学试卷(4)(解析版)
题型:解答题
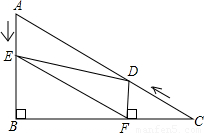
如图,在Rt△ABC中,∠B=90°,BC=5
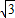
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:
来源:2012-2013学年新人教版九年级(上)期中数学试卷(6)(解析版)
题型:填空题
方程(x+1)(x-3)=0的解x1= ,x2= .
查看答案和解析>>
科目:
来源:2012-2013学年新人教版九年级(上)期中数学试卷(6)(解析版)
题型:填空题
(1)已知关于x的方程x2+3x+k=0的一个根是-1,则k= ;
(2)三角形的两边长分别为3和6,第三边的长是方程x2-6x+8=0的一个根,则这个三角形的周长是 .
查看答案和解析>>
科目:
来源:2012-2013学年新人教版九年级(上)期中数学试卷(6)(解析版)
题型:填空题
若正方形面积为24cm2,则它的边长是 cm;一条对角线长是 cm.
查看答案和解析>>


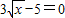 的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.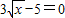
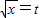 ,
,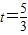
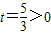
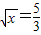 ,
,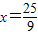 .
.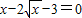
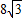 ,求AC的长.
,求AC的长.
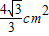 ,求旋转的角度n.
,求旋转的角度n.
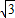 ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.