如图，AB∥DE，∠1＝25°，∠2＝110°，求∠BCD的度数．

问题探究：

(1)如果一个角的两条边与另一个角的两条边分别平行，那么这两个角的大小有何关系？举例说明．

(2)如果一个角的两边与另一个角的两边分别垂直，那么这两个角的大小有何关系？举例说明．

如图，DE∥BC，∠D∶∠DBC＝2∶1，∠1＝∠2，求∠E的度数．

已知：如图，AB∥CD，AP平分∠BAC，CP平分∠ACD，求∠APC的度数．

解：过P点作PM∥AB交AC于点M．

∵AB∥CD，(　　)

∴∠BAC＋∠________＝180°．(　　)

∵PM∥AB，

∴∠1＝∠________，(　　)

且PM∥________．(平行于同一直线的两直线也互相平行)

∴∠3＝∠________．(两直线平行，内错角相等)

∵AP平分∠BAC，CP平分∠ACD，(　　)

∴∠1＝∠________，∠4＝∠________．(　　)

∴∠1＋∠4＝∠BAC＋∠ACD＝90°．(　　)

∴∠APC＝∠2＋∠3＝∠1＋∠4＝90°．(　　)

总结：两直线平行时，同旁内角的角平分线________．

已知：如图，四边形ABCD中，AB∥CD，AD∥BC，∠B＝50°．求∠D的度数．

分析：可利用∠DCE作为中间量过渡．

解法1：∵AB∥CD，∠B＝50°，(　　)

∴∠DCE＝∠________＝________°．

(________，________)

又∵AD∥BC，(　　)

∴∠D＝∠________＝________°．(________，________)

想一想：如果以∠A作为中间量，如何求解？

解法2：∵AD∥BC，∠B＝50°，(　　)

∴∠A＋∠B＝________．(________，________)

即∠A＝________－________＝________°－________°＝________°．

∵DC∥AB，(　　)

∴∠D＋∠A＝________．(________，________)

即∠D＝________－________＝________°－________°＝________°．

已知：如图，AB∥CD，∠B＝35°，∠1＝75°．求∠A的度数．

解题思路分析：欲求∠A，只要求∠ACD的大小．

解：∵CD∥AB，∠B＝35°，(　　)

∴∠2＝∠________＝________°．(________，________)

而∠1＝75°，

∴∠ACD＝∠1＋∠2＝________°．

∵CD∥AB，(　　)

∴∠A＋________＝180°．(________，________)

∴∠A＝________＝________．

已知：如图，AB∥CD，∠1＝∠2．求证：BE∥CF．

证明思路分析：欲证BE∥CF，只要证________＝________．

证明：∵AB∥CD，(　　)

∴∠ABC＝________．(________，________)

∵∠1＝∠2，(　　)

∴∠ABC－∠1＝________－________，(　　)

即________＝________．

∴BE∥CF．(________，________)

已知：如图，AB∥CD，∠1＝∠B．

求证：CD是∠BCE的平分线．

证明思路分析：欲证CD是∠BCE的平分线，

只要证________＝________．

证明：∵AB∥CD，(　　)

∴∠2＝________．(________，________)

但∠1＝∠B，(　　)

∴________＝________．(等量代换)

即CD是________．

已知：如图，∠1＋∠2＝180°．求证：∠3＝∠4．

证明思路分析：欲证∠3＝∠4，只要证________∥________．

证明：∵∠1＋∠2＝180°，(　　)

∴________∥________．(________，________)

∴∠3＝∠4．(________，________)

如图，∠1＝∠2，∠3＝110°，求∠4．

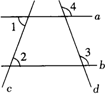
解题思路分析：欲求∠4，需先证明________∥________．

解：∵∠1＝∠2，(　　)

∴________∥________．(________，________)

∴∠4＝________＝________°．(________，________)