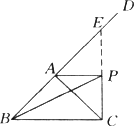
一个数学课外活动小组进行野外测量，如图所示，张华站在B处，小李站在C处，秦辉站在A处，赵明站在∠CAD的平分线上的P处．最后一个同学说：我不用测量就知道赵明到张华，赵明到小李之间的距离之和大于秦辉与张华，秦辉与小李之间的距离和．你能确定这个同学的说法有道理吗？

某铁路施工队要打通一座小山建隧道，如图设计时要测隧道的长度，恰好山前是一片空地，利用这样有利地形，测量人员是否可以利用三角形全等的知识测量出隧道长度，画出你设计的测量方法图，并说明道理．

如图，这是一个平分角的仪器，其中AB＝AD，BC＝DC．将点A放在角的顶点，AB和AD沿着角的两边放下．沿AC画一射线AE，AE就是角平分线，你能说明其中的道理吗？

我军在前进途中被大河挡住去路(如图所示)，当时部队没有任何测量工具，一战士仅用头上戴的军帽和一条绳子测得了河宽，使部队顺利架起浮桥．

(1)这名战士如何测得河宽？

(2)你有不同方法吗？

在一次战役中，如图所示，我军阵地与敌军碉堡隔河相望．为炸掉它，需知我军阵地与碉堡的距离，在不能过河测量又没有任何测量工具的情况下，一个战士想出一个办法，他面向碉堡方向站好，然后调整帽子，使视线通过帽檐正好落在碉堡的底部，然后，他转过一个角度，保持刚才姿态，这时视线落在自己所在岸的某一点上，接着，他用步测的办法量出自己与那个点的距离，这个距离就是他与碉堡间的距离．

(1)按这个战士的方法，找出教室或操场与你距离相等的两个点，并通过测量加以验证．

(2)你能解释其中的道理吗？

育才中学七年级(二)班学生到野外活动．为测量一池塘两端A、B的距离，设计了如下几种方案：(Ⅰ)如图A所示先在平地取一个可以直接到达A、B的点C，可连结AC、BC，并分别延长AC至D、BC至E，使DC＝AC，EC＝BC．最后测出DE的距离即为AB之长．(Ⅱ)(如图B所示)先过B点作AB的垂线BF，再在BF上取C、D两点，使BC＝CD．接着过点D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为A、B的距离．

阅读后回答下列问题：

(1)方案(Ⅰ)是否可行？________，理由是________．

(2)方案(Ⅱ)是否切实可行？________，理由是________．

(3)方案(Ⅱ)中作BF⊥AB，ED⊥BF的目的是________；若仅满足∠ABD＝∠BDE≠90°，方案(Ⅱ)是否成立？________．

市政建筑公司计划要在学校东面分别建造一座桥和一个汽车站，桥在汽车站北面，现已知学校到桥，桥到汽车站及学校到汽车站距离分别为250米，500米，500米，请根据以上提示确定桥与汽车站分别应建在何处？在图纸上标出来．

暑假里，王平回老家潍坊．爷爷正在做风筝，王平顺手拿起一个用六根竹条连接而成的凸六边形风筝骨架，但它并不稳固，王平对爷爷说：“这样的风筝能飞上天吗？”爷爷笑哈哈的说：“你能再加上三根竹条与顶点连接，使它变得又稳定又对称吗？”王平想了想，给风筝接上了三根竹条，这个风筝稳稳的了，你能在图①②中分别加上三根竹条，设计出两种不同的连接方案(用直尺连接)吗？

如图，已知AC＝BD，AB＝CD，试判断OA与OD的关系，说明理由．

小明做了一个如图所示的风筝，他想去验证∠BAC与∠DAC是否相等，但手头却只有一把足够长的尺子，你能帮助他想个办法吗？说明你这样做的理由？